Содержание
Документы —
Правительство России
Варианты поиска по сайту
Закрыть
Следующая новость
Предыдущая новость
- Маленький размер шрифта
- Нормальный размер шрифта
- Большой размер шрифта
- Включить/выключить отображение изображений
Вкл
Выкл
Правительство России
- Демография
- Здоровье
- Образование
- Культура
- Общество
- Государство
- Занятость и труд
- Технологическое развитие
- Экономика.
Регулирование - Финансы
- Социальные услуги
- Экология
- Жильё и города
- Транспорт и связь
- Энергетика
- Промышленность
- Сельское хозяйство
- Региональное развитие
- Дальний Восток
- Россия и мир
- Безопасность
- Право и юстиция
- Избранные документы со справками к ним
- Поиск по всем документам
Вид документа
Постановление Правительства Российской ФедерацииРаспоряжение Правительства Российской ФедерацииРаспоряжение Президента Российской ФедерацииУказ Президента Российской ФедерацииФедеральный законФедеральный конституционный законКодекс
Номер
Заголовок или текст документа
Дата подписания
23 ноября, среда
Постановление Правительства Российской Федерации от 23.
11.2022 г. № 2116
О внесении изменения в пункт 1 постановления Правительства Российской Федерации от 22 декабря 2021 г. № 2389
22 ноября, вторник
Постановление Правительства Российской Федерации от 22.11.2022 г. № 2113
О внесении изменения в пункт 2 постановления Правительства Российской Федерации от 31 марта 2022 г. № 542
Постановление Правительства Российской Федерации от 22.11.2022 г. № 2108
Об утверждении Правил размещения указаний, предусмотренных частями 3 и 4 статьи 9 Федерального закона «О контроле за деятельностью лиц, находящихся под иностранным влиянием», в том числе требований к их размещению, а также форм указаний, предусмотренных частями 3 и 4 статьи 9 Федерального закона «О контроле за деятельностью лиц, находящихся под иностранным влиянием»
Постановление Правительства Российской Федерации от 22.
11.2022 г. № 2110
О внесении изменений в Положение о порядке выплаты страховой пенсии лицам, выезжающим (выехавшим) на постоянное жительство за пределы территории Российской Федерации
Постановление Правительства Российской Федерации от 22.11.2022 г. № 2107
О внесении изменения в Правила выдачи разрешения на включение в наименование некоммерческой организации официального наименования «Российская Федерация» или «Россия», а также слов, производных от этого наименования
Постановление Правительства Российской Федерации от 22.
11.2022 г. № 2105
О внесении изменений в постановление Правительства Российской Федерации от 29 октября 2022 г. № 1923
19 ноября, суббота
Постановление Правительства Российской Федерации от 19.11.2022 г. № 2100
О внесении изменений в Правила определения численности застрахованных лиц в целях формирования бюджета Федерального фонда обязательного медицинского страхования, бюджетов субъектов Российской Федерации и бюджетов территориальных фондов обязательного медицинского страхования
Постановление Правительства Российской Федерации от 19.
11.2022 г. № 2099
О внесении изменений в государственную программу Российской Федерации «Развитие туризма»
18 ноября, пятница
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2097
О признании утратившим силу пункта 6 изменений, которые вносятся в акты Правительства Российской Федерации, утвержденных постановлением Правительства Российской Федерации от 17 декабря 2021 г. № 2341
Постановление Правительства Российской Федерации от 18.
11.2022 г. № 2095
О внесении изменений в постановление Правительства Российской Федерации от 27 октября 2008 г. № 795
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2091
О внесении изменений в постановление Правительства Российской Федерации от 25 декабря 2009 г. № 1093
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2098
О внесении изменений в постановление Правительства Российской Федерации от 15 марта 2021 г.
№ 379
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2094
О внесении изменений в некоторые акты Правительства Российской Федерации
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2090
О внесении изменений в Классификацию основных средств, включаемых в амортизационные группы
Постановление Правительства Российской Федерации от 18.
11.2022 г. № 2096
О внесении изменений в постановление Правительства Российской Федерации от 5 апреля 2022 г. № 591
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2089
О внесении изменений в подпункт «д» пункта 1 изменений, которые вносятся в акты Правительства Российской Федерации, утвержденных постановлением Правительства Российской Федерации от 18 апреля 2022 г. № 695
Постановление Правительства Российской Федерации от 18.
11.2022 г. № 2092
О внесении изменений в постановление Правительства Российской Федерации от 25 декабря 2009 г. № 1092
Постановление Правительства Российской Федерации от 18.11.2022 г. № 2093
Об утверждении Правил предоставления субсидий из федерального бюджета производителям деревянных домокомплектов на возмещение выпадающих доходов, связанных с предоставлением скидки физическим лицам на покупку таких деревянных домокомплектов
17 ноября, четверг
Постановление Правительства Российской Федерации от 17.
11.2022 г. № 2087
О внесении изменений в Правила определения технологии в качестве наилучшей доступной технологии, а также разработки, актуализации и опубликования информационно-технических справочников по наилучшим доступным технологиям
Постановление Правительства Российской Федерации от 17.11.2022 г. № 2084
Об освобождении от предоставления обеспечения исполнения обязанности по уплате таможенных пошлин, налогов в отношении отдельных категорий товаров
1
Показать еще
Уклон плоских крыш — База знаний ТЕХНОНИКОЛЬ
Уклон крыши необходим для эффективного отвода воды с поверхности ската.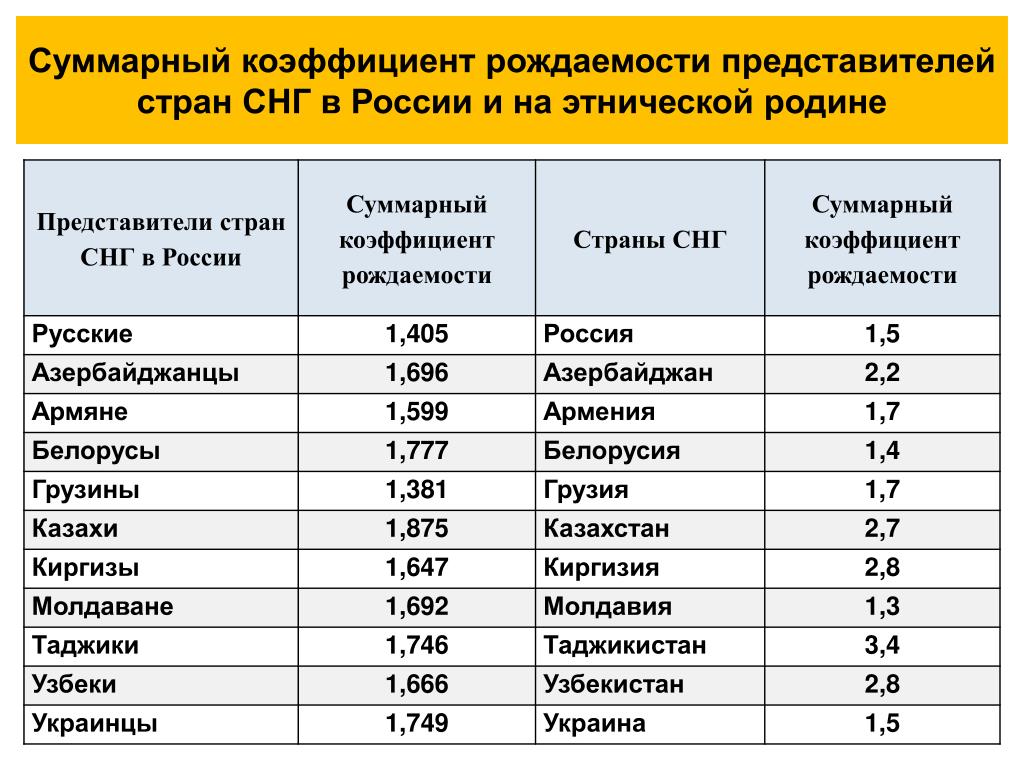
При нарушении уклона крыши образуются застойные зоны, которые способствуют сокращению срока службы водоизоляционного ковра.
Крыша с большим уклоном «прощает» мелкие ошибки при монтаже и увеличивает срок службы конструкции.
В чем измеряется уклон крыши
Уклоном называют величину крутизны ската крыши.
Если представить крышу в разрезе, то получится прямоугольный треугольник. Уклоном будет считаться тангенс угла α, который равен отношению противолежащего катета к прилежащему.
Уклон может измеряться в градусах – °, процентах – %, а также может быть выражен коэффициентом уклона i.
Крыши с уклоном до 12° принято считать плоскими, а с уклоном 12° и более — скатными.
Перевод уклона из градусов в проценты
Для перевода уклона из градусов в проценты следует тангенс угла в градусах умножить на 100:
Для перевода уклона из процентов в градусы следует вычислить функцию арктангенса угла в процентах, умноженного на 0,01:
Сводная таблица с уклонами в различных величинах
Коэффициент уклона, i | Угол наклона, ° | Наклон, % |
0,008 | 0,5 | 0,8 |
0,01 | 0,6 | 1,0 |
0,015 | 0,9 | 1,5 |
0,02 | 1,1 | 2,0 |
0,03 | 1,7 | 3,0 |
0,05 | 2,9 | 5,0 |
0,10 | 5,7 | 10,0 |
0,12 | 6,8 | 12,0 |
0,15 | 8,5 | 15,0 |
0,20 | 11,3 | 20,0 |
0,25 | 14 | 25,0 |
0,30 | 16,7 | 30,0 |
0,45 | 24,2 | 45,0 |
0,60 | 31 | 60,0 |
1,00 | 45 | 100,0 |
Минимальный уклон крыши
В соответствии с действующими нормативными документами в строительстве, устройство скатов крыши необходимо выполнять с уклоном не менее 1,5% (i=0,015, 0,9°), т.
е. 1,5 см подъема ската крыши на 100 см длины.
Как определить минимальный коэффициент статического трения
Обновлено 14 декабря 2020 г.
Автор Chris Deziel
Трение — это сила, противодействующая движению. Физики различают статическое трение, которое удерживает тело в покое, и кинетическое трение, которое замедляет его движение, когда оно начинает двигаться. Сила трения покоя ( F s ) пропорциональна перпендикулярной силе, действующей телом на поверхность, по которой оно движется, которая называется нормальной силой ( F N ). Коэффициент пропорциональности называется коэффициентом статической доли, который обычно обозначается греческой буквой мю с нижним индексом s ( µ s ). Математическое соотношение:
F_s=\mu_s F_N
Этот коэффициент зависит от характеристик двух поверхностей, находящихся в контакте друг с другом. Он был приведен в таблицу для ряда различных материалов.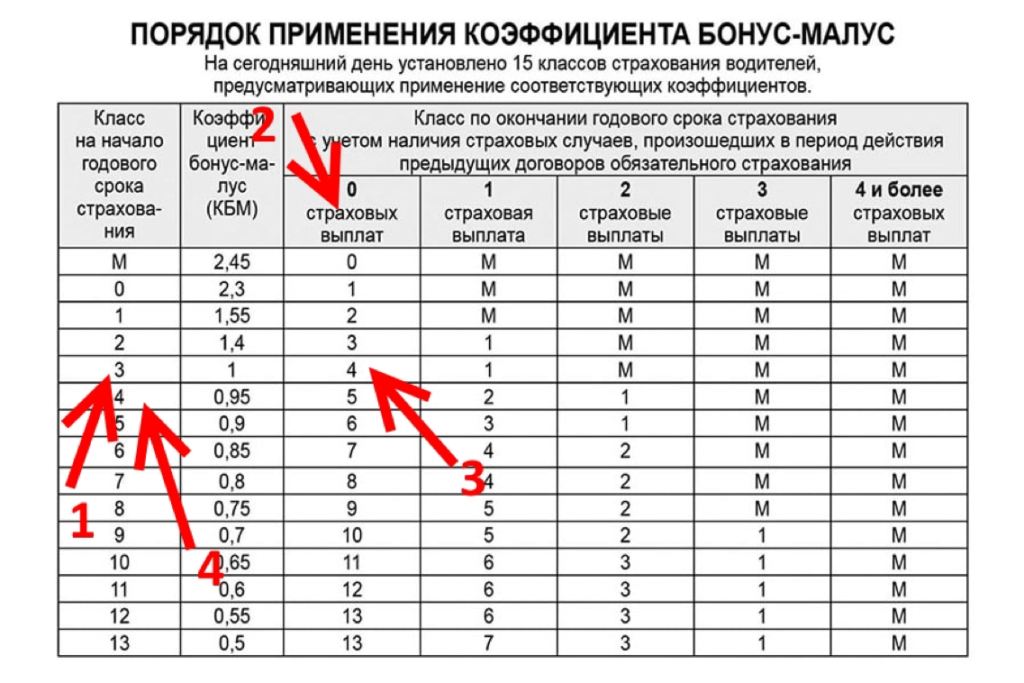
Если вы не можете найти µ s для материалов, которые вы используете, вы можете определить это с помощью простого эксперимента.
TL;DR (слишком длинный; не читал)
TL;DR (слишком длинный; не читал)
Чтобы найти минимальный коэффициент статического трения между двумя материалами, постройте наклонную плоскость из одного из материалов и поместите на него тело из другого материала. Увеличивайте угол наклона, пока тело не начнет скользить. Тангенс угла есть коэффициент трения.
Используйте наклонную плоскость
Простой способ определить µ s — поместить рассматриваемый объект на наклонную плоскость, изготовленную из того же материала, что и изучаемая поверхность. Постепенно увеличивайте угол наклона, пока объект не начнет скользить. Запишите этот угол. Вы можете сразу найти µ s потому что оно равно тангенсу угла.
И вот почему:
Когда вы поднимаете угол наклона, сила тяжести, действующая на тело массой м имеет горизонтальную и вертикальную составляющие. Применяя закон Ньютона к каждому из них непосредственно перед тем, как тело начинает двигаться, вы обнаружите, что горизонтальная составляющая (действующая в направлении x ) равна F x = ma x . То же верно и в направлении y : F y = ma y .
Ускорение в x -направлении, ma x , равно силе тяжести, которая представляет собой произведение массы на ускорение под действием силы тяжести ( г ) и синус угла ( ø ), образованного в точке опоры наклона. Поскольку тело не движется, это равно противодействующей силе трения покоя, и вы можете написать:
1. mg\sin{\theta}=F_s
ma y , равно косинусу угла, умноженному на массу, умноженной на ускорение свободного падения, и это должно быть равно нормальной силе, поскольку тело не движется,
2.
F_N=mg\cos{\theta}
Помните, что F s = µ s F N . Подставим F s в уравнение (1):
mg\sin{\theta}=\mu_s F_N
и используем равенство в уравнении (2) для замены F N :
mg\sin{\theta}=\mu_s mg \cos{\theta}
Термин « mg » сокращается с обеих сторон:
\mu_s=\frac{\sin{\theta }}{\cos{\theta}}=\tan{\theta}
6. СИЛА И ДВИЖЕНИЕ — II
6. СИЛА И ДВИЖЕНИЕ — II
- СИЛА И ДВИЖЕНИЕ — II
- 6.1. Статическое и кинетическое трение
- 6.2. Сила сопротивления
- 6.3. Равномерное круговое движение
- 6.4. Округление кривой
Рисунок 6.1. Статическое трение.
Предположим, что к бруску, лежащему на шероховатой поверхности, приложена горизонтальная сила F.
поверхность (см.
рис. 6.1). Пока приложенная сила F меньше
определенное максимальное усилие (F max ), блок не будет двигаться. Это означает
что результирующая сила, действующая на блок в горизонтальном направлении, равна нулю.
Следовательно, кроме приложенной силы F, должна действовать вторая сила f.
на блоке. Сила f должна иметь силу, равную F, и должна быть
указывая в противоположном направлении. Эта сила f называется силой трения,
и поскольку блок не двигается, мы имеем дело со статической
трение . Эксперименты показали, что сила трения покоя
в значительной степени не зависит от площади контакта и пропорциональна нормальной силе
N, действующий между блоком и поверхностью. Сила трения покоя равна
f <= u с N
где u s коэффициент статического трения
(что безразмерно). Коэффициент статического трения составляет примерно
постоянная (независимая от N). Максимальная сила, которую можно приложить без
перемещение блока
F max = u s N
Как только блок пришел в движение, сила F, необходимая для его удержания,
при движении с постоянной скоростью обычно меньше критической силы
необходимо для начала движения.
В данной ситуации мы имеем дело с
кинетическое трение и сила трения f k определяется выражением
f k = u k N
где u k коэффициент кинетического трения .
Кинетическая сила трения не зависит от приложенной силы, но всегда
указывает в противоположном направлении. Уравнение для f k равно , а не
векторное уравнение , так как f k и N не указывают на одно и то же
направление.
Примечание: Трение между автомобильными шинами и дорогой является трением покоя.
Это трение имеет решающее значение, когда вы пытаетесь остановить автомобиль. Так как максимальный статический
сила трения больше кинетической силы трения, автомобиль можно остановить
быстрее всего, если мы предотвратим блокировку колес. Когда колеса блокируются,
сила трения меняется на кинетическую трение (шины и земля соприкасаются).
движутся относительно друг друга), тем самым уменьшая ускорение и
увеличение времени и длины, необходимых для остановки автомобиля.
Пример задачи 6-1
На рис. 6.2 показана масса m на наклонном склоне. Под определенным углом [тета]
масса начинает скатываться по склону. Рассчитать коэффициент статичности
трение.
Рисунок 6.2. Система координат, используемая в примере задачи 1.
На рис. 2 показана система координат, используемая в этой задаче. Обратите внимание, что с
этот выбор системы координат, нормальная сила N и сила трения f
иметь каждый только один компонент; N направлен вдоль оси Y, а f направлен
по оси x. Так как это максимальный угол, под которым объект будет
остаются в покое, сила трения достигла своего максимального значения:
Поскольку объект покоится, результирующая сила, действующая на объект, равна нулю:
С точки зрения компонентов чистой силы вдоль оси x и
ось Y:
Из них легко получить коэффициент трения покоя.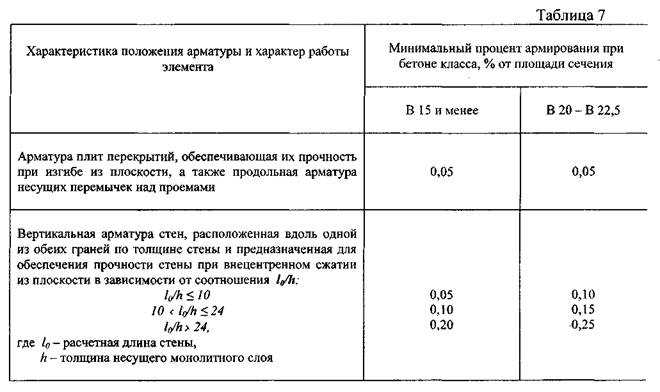
два уравнения:
Примечание Сила трения между автомобильными шинами и дорогой составляет
уменьшается, когда автомобиль движется вверх или вниз по склону. Ехать в гору сложнее
или под гору, когда дороги скользкие, чем ехать по ровной поверхности.
Рисунок 6.3. Диаграмма свободного тела для саней.
Пример задачи 6-3
Женщина тянет нагруженные сани (масса m) по горизонтальной поверхности с постоянной скоростью.
скорость. Коэффициент кинетического трения между полозьями и снегом равен
ты k и угол между веревкой и горизонтальной осью [phi]
(см. рис. 6.3). Чему равно натяжение веревки?
Так как сани движутся с постоянной скоростью, то результирующая сила на салазках
должен быть равен нулю. Разложение чистой силы на составляющие по оси x
и оси ординат, получаем следующие уравнения силы:
Второе уравнение можно использовать для исключения N:
Подставляя это выражение в первое уравнение получаем:
Теперь можно рассчитать натяжение T:
Нормальная сила N всегда перпендикулярна поверхности.
В двух предыдущих примерах нормальная сила N была пропорциональна
вес предмета. Однако это не всегда так. Например, предположим
Я прижимаю ластик к доске. Я спрашиваю себя, что такое
минимальная сила, которую мне нужно приложить, чтобы предотвратить соскальзывание ластика
? Эта ситуация схематично показана на рис. 6.4. Так как ластик находится в
покоя, результирующая сила, действующая на него, должна быть равна нулю (и, следовательно, компоненты
результирующая сила как в направлении x, так и в направлении y должна быть равна нулю):
Рисунок 6.4. Ластик на черной доске.
Второе уравнение говорит нам, что сила трения покоя
f s должно быть равно W. Отсюда следует следующее для нормального
сила Н:
Однако нормальная сила N равна приложенной силе F. Чтобы
чтобы ластик не соскальзывал, сила F должна превышать минимум
порог:
Это соотношение показывает, что если увеличить массу ластика,
усилие, необходимое для предотвращения соскальзывания ластика, увеличится (
минимальная сила пропорциональна массе).
Этот пример также иллюстрирует
ситуация, в которой нормальная сила не связана с массой объекта.
Рисунок 6.5. Задача 25П.
Проблема 25P
На рис. 6.5, А и В — блоки с весами 44 Н и 22 Н,
соответственно. (a) Определите минимальный вес блока C , который должен быть
помещается на A , чтобы предотвратить скольжение, если u s между A
а таблица 0,20. (b) Блок C внезапно отрывается от A .
Каково ускорение блока A , если u k между A
а таблица 0,15?
Груз (блок C) помещается сверху блока A и препятствует его скольжению.
Таким образом, ускорение системы равно 0 м/с 2 . Следовательно,
результирующая сила на каждом блоке равна 0 Н. Чтобы определить минимальную
вес блока C, необходимый для этого, мы начинаем вычислять сеть
усилие на каждом блоке. Силы, действующие на блок B, вес W B
и натяжение Т, схематично показаны на рис.
6.6. Чистая сила
действующая на блок B, направлена по оси ординат и имеет величину, равную
Рисунок 6.6. Силы, действующие на блок Б.
Поскольку результирующая сила, действующая на блок B, должна быть равна нулю, мы заключаем, что
T = W B
Силы, действующие на блок А и блок С, указаны на рис. 6.7.
Суммарная сила, действующая в направлении y, равна нулю и, следовательно,
Н = W A + W C
Поскольку система остается в покое, результирующая сила, действующая на блок А и
C вдоль оси x также должен быть равен нулю. Это означает, что статическое трение
сила f с должно быть равно натяжению T. Эксперименты показывают, что
f s имеет максимальное значение, которое определяется нормальной силой N и
коэффициент статического трения u с
f с <= u с N = u с (W A
+ W C )
Минимальный вес блока C, который не позволит системе
проскальзывание можно обнаружить, потребовав, чтобы
u s (W A + W C ) >= f s =
Т = Ш В
и таким образом
Рисунок 6.
7. Силы, действующие на блоки А и С.
Когда блок C удаляется, сила трения покоя изменяется (поскольку
нормальная сила изменилась). Максимальная статическая сила трения теперь
u s W A = 8,8 Н, что меньше веса блока B.
Очевидно, что блок А будет скользить, и оба блока будут ускоряться. В этот момент
Сила трения, действующая на блок А, равна кинетической силе трения f к
величина которого равна
f k = u k N = u k W A
Суммарная сила, действующая на блок А, равна
.
Суммарная сила, действующая на блок B, равна
.
Исключив из этих двух последних уравнений натяжение T, получим для
ускорение а
Рисунок 6.8. Задача 36П.
Проблема 36P
Два груза, м 1 = 1,65 кг и м 2 =
3,30 кг, прикрепленный безмассовым стержнем, параллельным наклонной плоскости, на которой
они оба скользят (см.
рис. 6.8), движутся по плоскости с
м 1 прицепной м 2 . Угол наклона
30град.. Коэффициент кинетического трения между м 1 и
наклон u 1 = 0,226; что между м 2 и
наклон равен u 2 = 0,113. Вычислите (а) натяжение стержня и (б)
общее ускорение двух масс. (c) Как бы ответы на (a)
и (b) заменить, если м 2 прицепной м 1 ?
Силы, действующие на массу m 1 , схематично показаны на рис. 6.9.
Компоненты x и y чистой силы, действующей на m 1 задаются как
Рисунок 6.9. Силы, действующие на m 1 .
В выбранной системе координат ускорение вдоль
ось Y. Таким образом, нормальная сила N 1 должна быть равна
m 1 g cos([тета]). Это фиксирует кинетическую силу трения
f 1k = u 1k Н 1 = и 1к
m 1 g cos([тета])
Масса m 1 будет ускоряться вниз по склону с ускорением a.
Ускорение a связано с x-компонентой чистой силы, действующей на
масса m 1
Силы, действующие на массу m 2 , схематично показаны на рис.
Рисунок 6.10. Сила трения f 2k , действующая на массу m 2
можно легко определить (см. вычисление f 1k ):
f 2k = u 2k N 2 = u 2k
m 2 g cos([тета])
Х-компонента чистой силы, действующей на массу m 2 , равна
по
и связано с ускорением a массы m 2
Рисунок 6.10. Силы, действующие на m 2 .
Теперь у нас есть два уравнения с двумя неизвестными (a и T). Устранение
напряжения T из этих двух уравнений получаем следующее выражение для a
Подставляя значения приведенных параметров, находим, что a = 3,62
м/с 2 .
Теперь можно легко определить натяжение T в стержне
что равно 1,06 Н. Если масса m 1 и масса m 2
обратные, мы все равно получим то же ускорение, но напряжение в
стержень будет отрицательным (это означает, что стержень сжимается).
Сила трения, которую мы обсуждали до сих пор, действует, когда две поверхности соприкасаются.
сила, стремящаяся уменьшить скорость тел, движущихся в воздухе, очень велика.
аналогично силе трения; эта сила называется силой сопротивления. Перетаскивание
сила D, действующая на тело, движущееся по воздуху, равна
где A – эффективная площадь поперечного сечения тела, [rho] –
плотность воздуха и v — скорость объекта. C — безразмерное сопротивление
коэффициент, который зависит от формы объекта и значение которого обычно
находится в пределах от 0,5 до 1,0. Направление силы сопротивления равно
противоположно направлению скорости.
Рисунок 6.11. Сила сопротивления.
Из-за силы сопротивления падающее тело в конце концов упадет с
постоянной скорости, так называемая конечная скорость v т . Когда
объект движется с конечной скоростью v t результирующая сила, действующая на него
должен быть равен нулю (отсутствие изменения скорости означает отсутствие ускорения). Это происходит, когда Д
= mg, а конечная скорость v t должна удовлетворять следующему
отношение:
и v t вычисляется как
Уравнение для v t показывает, что конечная скорость
объект увеличивается с уменьшением эффективной площади.
Конечная скорость объекта — это конечная скорость, которую он приобретает во время
свободное падение. Объект получит эту скорость независимо от того,
начальная скорость больше или меньше конечной скорости (см.
рис.
6.11).
В главе 4 мы видели, что когда частица движется по окружности, она
испытывает ускорение а, направленное к центру окружности, с
величина равна
где v — скорость частицы, r — радиус
круг. Ускорение a называется центростремительным.
ускорение . Чтобы учесть центростремительное ускорение,
На этот объект должна действовать центростремительная сила . Этот
сила должна быть направлена к центру окружности и может быть рассчитана
из второго закона Ньютона:
Примером равномерного кругового движения является движение
Луны вокруг Земли. Предположим, что период этого движения равен T. Что
говорит ли это нам о расстоянии r между Землей и Луной? В течение
за один период Луна проходит полное расстояние, равное 2[pi]r. Скорость
луна, т. м , можно рассчитать:
Соответствующая центростремительная сила равна
.
Здесь мы приняли, что m m — это масса Луны.
центростремительная сила обеспечивается гравитационным притяжением между землей
и луна. В главе 15 мы увидим, что сила гравитационного
взаимодействие можно рассчитать следующим образом:
где G — гравитационная постоянная, а m e — масса
Земля. Для постоянного кругового движения сила тяжести должна
обеспечить необходимую центростремительную силу:
Таким образом, расстояние между Землей и Луной может быть
рассчитано:
Известно, что гравитационная постоянная равна G = 6,67 x 10 -11
m 3 /(s кг), а масса Земли известна как m e =
5,98 х 10 24 кг. Измеренный период Луны составляет 27,3 дня (2,3 х
10 6 с). Таким образом, расстояние между Луной и Землей может
вычислить:
r = 3,82 x 10 8 м
что хорошо согласуется с расстоянием, полученным с использованием других методов
(например, измерение времени, которое требуется свету для прохождения от
Земля на Луну и обратно).
Рисунок 6.12. Силы, действующие на автомобиль при движении по кривой без уклона.
Трение имеет решающее значение, если мы хотим повернуть кривую во время вождения автомобиля или
велосипед. Это легко понять, если рассмотреть силы, действующие на
автомобиль во время поворота. Предположим, что рассматриваемый автомобиль совершает поворот
с радиусом R и скоростью v. На рис. 6.12 показаны силы, действующие на автомобиль.
Движения в вертикальном направлении нет, и результирующая сила в этом
Поэтому направление должно быть равно нулю. Это требует, чтобы нормальная сила
N равно весу автомобиля:
Н = м г
Когда автомобиль огибает кривую, он совершает равномерное круговое движение.
Соответствующее центростремительное ускорение этого движения равно
Для того чтобы автомобиль совершал это круговое движение, должно существовать
радиальная сила с силой, равной
Эта сила может быть обеспечена только силой трения покоя и
поэтому мы требуем, чтобы
Сила трения покоя f s имеет максимальное значение, равное
u s N и это ограничивает скорость и радиус кривизны
кривая, которую может пройти автомобиль:
Делаем вывод, что автомобиль сможет совершить поворот с радиусом R и
скорость v, если коэффициент трения покоя между шинами и дорогой
это
Рисунок 6.
13. Силы, действующие на автомобиль при движении по кривой.
Если на дороге нет трения (u s = 0) из-за покрытия
льда, машина вообще не сможет объехать ни одну кривую. Чтобы избежать
проблемы, как это, кривые на шоссе, как правило, накрен. Эффект
банковские кривые могут быть легко поняты. На рис. 6.13 показаны силы
действует на автомобиль, когда он огибает кривую на шоссе с наклоном. Мы
Предположим, что трения между шинами и дорогой нет. Нормальный
сила N имеет составляющие как по радиальной, так и по вертикальной осям. С
движение по вертикали отсутствует, результирующая сила вдоль
вертикальная ось должна быть равна нулю. Для этого требуется
и фиксирует нормальную силу Н
Радиальная составляющая нормальной силы определяется как
Эта составляющая нормальной силы может создавать радиальное ускорение
требуется, чтобы позволить автомобилю огибать кривую даже при отсутствии трения.
Если автомобиль должен объехать кривую радиусом R и со скоростью v, нам потребуется
что
или
Это последнее уравнение показывает, что угол крена кривой шоссе равен
рассчитаны на определенную скорость и радиус кривизны.
Пример задачи 6-9
Конический маятник вращается по горизонтальной окружности с постоянной скоростью v при
конец шнура, длина которого L. Шнур образует угол [тета] с
вертикальный. Каков период маятника?
Маятник схематично показан на рис. 6.14. Так как маятник
совершая равномерное движение по окружности, ускорение маятника должно
указать на центр окружности (направление вдоль вектора положения r)
а модуль ускорения равен v 2 /r, где v —
скорость маятника, а r — радиус окружности. Чистая сила в
поэтому горизонтальная плоскость всегда должна быть направлена к центру
окружности и имеют силу, определяемую вторым законом Ньютона.
Система координат выбрана так, что начало координат совпадает с центром
окружности, описывающей движение маятника. Так как горизонталь
составляющая силы всегда направлена к центру, который мы будем использовать
ось r (а не ось x). Ось Y совпадает с вертикалью
направлении (см. рис. 6.14). Поскольку координата y боба постоянна,
ускорение в направлении y должно быть равно нулю. Чистая сила в этом направлении
поэтому должен быть равен нулю:
Это выражение позволяет рассчитать натяжение T:
Теперь можно определить результирующую силу в радиальном направлении:
Рисунок 6.14. Пример задачи 6-9.
Теперь можно рассчитать центростремительное ускорение a:
Из радиуса R траектории и центростремительного ускорения a,
можно рассчитать скорость объекта:
Период T можно рассчитать по известным скорости v и радиусу
Р:
Для L = 1,7 м и [тета] = 37 град.
период Т = 2,3 с.
Пример задачи 6-10
Кадиллак массой m движется с постоянной скоростью v по криволинейной траектории.
(без насыпи) проезжей части, радиус кривизны которой равен R. Каков минимальный
коэффициент статического трения u s между шинами и дорожным полотном
?
Рисунок 6.15. Пример задачи 6-10.
Ситуация схематично показана на рис. 6.15. Так как есть
нет ускорения в направлении y, результирующая сила в этом направлении должна быть
ноль:
Центростремительная сила F c определяется как:
В этом случае центростремительная сила обеспечивается статической
сила трения. Если проскальзывание не происходит, максимальная сила статического трения должна
превышает требуемую центростремительную силу:
Из этого можно получить минимальный коэффициент статического трения.
уравнение:
Если скорость автомобиля 72 км/ч (20 м/с), а радиус
кривизна R = 190 м, минимальное значение коэффициента трения покоя равно
0,21. Обратите внимание, что масса автомобиля в расчет не входит, а
Таким образом, коэффициент трения одинаков для всех тел, движущихся с одинаковой скоростью.
скорость. Минимальный коэффициент статического трения масштабируется с квадратом
скорость; уменьшение скорости в два раза уменьшит
минимальный коэффициент трения в четыре раза.
Проблема 58E
Каскадер ведет машину по вершине холма, поперечное сечение которого
может быть аппроксимирована окружностью радиусом 250 м. Какая наибольшая скорость у
который он может проехать, не съезжая с дороги на вершине холма?
Автомобиль не сойдет с дороги на вершине холма, если результирующая радиальная сила
действуя на него, можно обеспечить требуемое центростремительное ускорение. Единственный радиальный
Силы, действующие на автомобиль, — это сила тяжести и нормальная сила (см.
Рисунок 6.16). Чистая радиальная сила F r действует на автомобиль равно
до
Рисунок 6.16. Силы, действующие на автомобиль.
F r = W — N
Поскольку нормальная сила N всегда направлена вдоль положительной оси y,
радиальная сила никогда не превысит вес автомобиля W. Поэтому это
также ограничивает центростремительную силу и, следовательно, скорость автомобиля.
Теперь можно легко найти максимальную скорость автомобиля
Предположим, что автомобиль движется со скоростью менее 178 км/ч.
теперь можно вычислить нормальную силу N, и она будет функцией скорости v.
Если автомобиль совершает равномерное круговое движение, то мы знаем, что чистый радиальный
на него должна действовать сила и что его величина равна mv 2 /R.
Суммарная радиальная сила, действующая на автомобиль, равна W — N.
Мы заключаем, что
или
Проблема 60P
Небольшой предмет помещают на расстоянии 10 см от центра фонографа.
Проигрыватель. Наблюдается, что он остается на столе, когда он вращается на 33 1/3.
оборотов в минуту, но соскальзывает, когда вращается со скоростью 45 оборотов в минуту.
минута. В каких пределах должен находиться коэффициент трения покоя между
объект и поверхность поворотного стола лежат ?
Объект расположен на расстоянии R от оси вращения. В течение одного
оборота объект проходит расстояние 2piR. Если совершить один оборот
за время T линейная скорость объекта может быть получена с помощью
следующее уравнение:
Чтобы объект совершал такое равномерное круговое движение,
должен обеспечивать радиальную силу величиной равной
Единственная радиальная сила, действующая на объект, — это трение покоя.