Содержание
Если пересек сплошную линию разметки, засыпанную снегом, что мне за это будет? — журнал За рулем
Обильный снегопад очень быстро скрывает под собой следы человеческой активности на асфальте – речь, разумеется, идет о дорожной разметке, которой призывают руководствоваться ПДД. И тогда у многих водителей возникает резонный вопрос: а могут ли оштрафовать за нарушение невидимой разметки?
Казалось бы, нет разметки – нет и нарушения. По крайней мере, здравый смысл подталкивает именно к такому умозаключению. Однако не все так просто. Например, камеры видеофиксации, которые в изобилии появились на улицах городов, могут зафиксировать пересечение сплошной линии даже в том случае, если ее не видно. Дело в том, что они ориентируются по виртуальной разметке, которая зашита в программе; посему решение о нарушении электроника принимает, основываясь на собственных показаниях, которые не всегда объективны. И хотя в «письмах счастья» всегда указан инспектор, который выносит то или иное постановление, в действительности система работает в автоматическом режиме. Это значит, что вы вправе оспорить такой штраф, если визуально факт нарушения не очевиден: в конце концов, вы же не можете видеть сквозь снег!
Это значит, что вы вправе оспорить такой штраф, если визуально факт нарушения не очевиден: в конце концов, вы же не можете видеть сквозь снег!
Нечитаемые знаки и разметка: как выиграть битву с невидимками
Однако надо понимать, что невидимая разметка – это не повод лезть на рожон и, например, ездить по встречке как вам заблагорассудится. Да, в теории, если разделительную сплошную (или двойную сплошную) качественно замело, а никаких знаков, запрещающих обгон, вы не наблюдаете (может, их тоже замело?) и готовы атаковать попутку, то, будучи пойманным инспектором, вы с изрядной долей вероятности сможете доказать в суде свою правоту. Но ежели разметка худо-бедно, но все-таки видна, то судья вряд ли встанет на вашу сторону. Так что, если вас «приняли» за встречку и дело пахнет судебным разбирательством, то озаботьтесь доказательствами собственной невиновности и тщательно сфотографируйте на смартфон дорогу и расположение на ней как своей машины, так и автомобиля ДПС и состояние дорожного покрытия.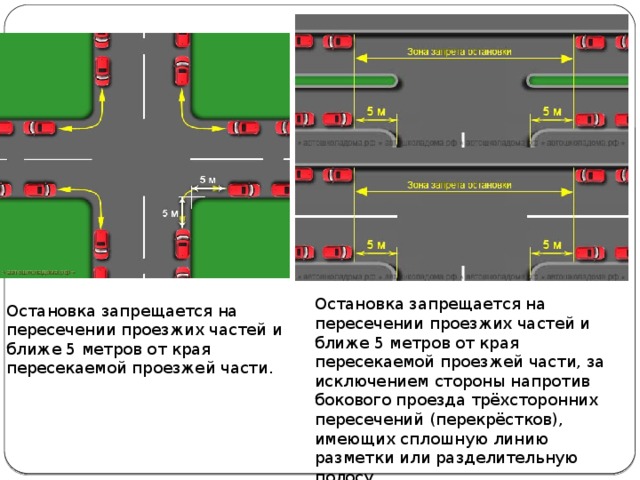 Вам же в плюс, если сможете приобщить к делу видеозапись (например, с видеорегистратора), доказывающую вашу правоту.
Вам же в плюс, если сможете приобщить к делу видеозапись (например, с видеорегистратора), доказывающую вашу правоту.
И всегда держите в голове те пункты Правил дорожного движения, которыми следует руководствоваться, когда разметки не видно. Помните, что обгон запрещен не только там, где действует соответствующий знак, но и на перекрестках, пешеходных переходах, железнодорожных переездах; мостах, путепроводах, эстакадах и туннелях; а также на опасных поворотах и участках с ограниченной видимостью. На таких участках дороги проезжая часть обычно «украшена» сплошной линией.
Также Правила запрещают выезжать для обгона на встречную полосу на дорогах с двусторонним движением, имеющих четыре или более полосы. При этом определять количество полос придется на глазок (разметку-то не видно!) «с учетом ширины проезжей части, габаритов транспортных средств и необходимых интервалов между ними» – в соответствии с главой 9.1 ПДД.
Понравилась заметка? Подпишись и будешь всегда в курсе!
За рулем в Дзен
Штраф за пересечение двойной сплошной в Украине — сумма
Какой штраф за пересечение 2 сплошных в Украине в 2022 году и как оспорить санкции.
Еще с автошколы, каждый водитель знает, что пересекать двойную сплошную запрещено. Среди водителей даже бытует мнение, что за пересечение двойной сплошной могут забрать права, но это не совсем так. Как правило, водители идут на сознательное нарушение и пересекают двойную сплошную, чтобы не делать «лишние круги» и быстрее добраться до места назначения.
Читайте также: Обязан ли водитель платить штраф за не пристегнутого пассажира — ответ
Сегодня Bigmir)Авто подготовил для вас, материал о видах и размерах штрафа за пересечение двойной сплошной в Украине в 2022 году, а также мы поговорим о ситуации, когда за пересечение двойной сплошной у водителя могут забрать права.
Какой штраф за пересечение 2 сплошных в Украине в 2022 году
скриншот
Читайте также: Штраф за отсутствие техосмотра в Украине — детали
Согласно правилам дорожного движения, двойная сплошная — это горизонтальная разметка белого цвета под номером 1.3. В разделе 34 ПДД сказано, что это разметку нельзя пересекать в любом случае. Админкодекс предусматривает следующие наказания для водителей, которые не выполнили правила и решили пересечь двойную сплошную:
Админкодекс предусматривает следующие наказания для водителей, которые не выполнили правила и решили пересечь двойную сплошную:
- ч.1 ст. 122 предусматривает штраф в 340 грн за нарушение требований разметки
- ч. 5 ст. 122 предусматривает штраф в размере 1445 грн или лишение прав от 6 месяцев до 1 года за создание аварийной ситуации
Какой штраф за сплошную на камеру в Украине
Читайте также: В каких случаях водитель может получить устное замечание вместо штрафа
На сегодняшний день, единственной камерой автофиксации, которая фиксирует проезд по полосе общественного транспорта, является камера по адресу: Киев, бульвар Дружбы Народов 36. В зависимости от того, в каком именно положении нарушитель будет на дороге во время фиксации, ему грозят следующие санкции:
- ч.1 ст. 122 предусматривает штраф в 340 грн за нарушение требований разметки
- ч.
 3 ст. 122 предусматривает штраф в 680 грн за движение по полосе общественного транспорта
3 ст. 122 предусматривает штраф в 680 грн за движение по полосе общественного транспорта
Что бывает за пересечение сплошной линии в Украине
depositphotos
Читайте также: Мгновенная карма: водитель пролетел на красный и получил штраф
Сплошных линий согласно украинским ПДД может быть несколько видов:
- 1.1 — белая сплошная линия
- 1.2 — широкая белая сплошная линия
- 1.12 — стоп линия
Разметку белая сплошная линия (1.1) запрещено пересекать всегда, кроме случаев:
- когда этой линией обозначено место стоянки или площадку для парковки
- когда этой линией обозначен край проезжей части, смежный с обочиной
- объезда неподвижного препятствия, размеры которого не позволяют осуществить его безопасный объезд, не пересекая эту линию
- обгона одиночных транспортных средств, которые двигаются со скоростью менее 30 км/ч.

Широкую белую сплошную линию (1.2) запрещено пересекать всегда
За пересечение одной из этих сплошных линий водителю грозит наказание:
- ч.1 ст. 122 предусматривает штраф в 340 грн за нарушение требований разметки
Стоп-линию (1.12) запрещено пересекать, когда горит красный сигнал светофора или регулировщик показывает запрещающий сигнал.
За пересечение стоп-линии, когда это запрещено водителю грозит:
- ч.2 ст. 122 которая предусматривает штраф в 510 грн за проезд на запрещающий сигнал светофора или регулировщика
Какой штраф за пересечение двойной сплошной в Украине
depositphotos
За пересечение двойной сплошной линии (1.3) в Украине водителя могут оштрафовать по:
- ч.1 ст. 122 предусматривает штраф в 340 грн за нарушение требований разметки
- ч. 5 ст. 122 предусматривает штраф в размере 1445 грн или лишение прав от 6 месяцев до 1 года за создание аварийной ситуации
Подпишись на наш Telegram-канал, если хочешь первым узнавать главные новости
Вам также может быть интересно:
- В МВД хотят установить на дорогах 2500 камер автофиксации: подробности
- Меньше теории и ужесточенная практика: новая система подготовки водителей в Украине
- Украинцы смогут самостоятельно выбирать номера для авто: подробности
- Теги:
- штрафы
- нарушение ПДД
- разметка
- поворот через двойную сплошную
- советы водителям
Пересечения твердых тел — DCG
Пересечения твердых тел
|
Это распространенный экзаменационный вопрос, который может быть весьма удовлетворительным.
Это означает, что при некоторых приличных орфографических навыках и полуприличной способности визуализировать объект можно получить около 2/3 доступных оценок. Последняя 1/3 требует немного больше усилий, и вот навыки, которые вам понадобятся. |
Терминология
Вершина — заостренная вершина пирамиды или конуса
Точки изгиба — когда линия взаимопроникновения встречается с краем одной из фигур, она поворачивается.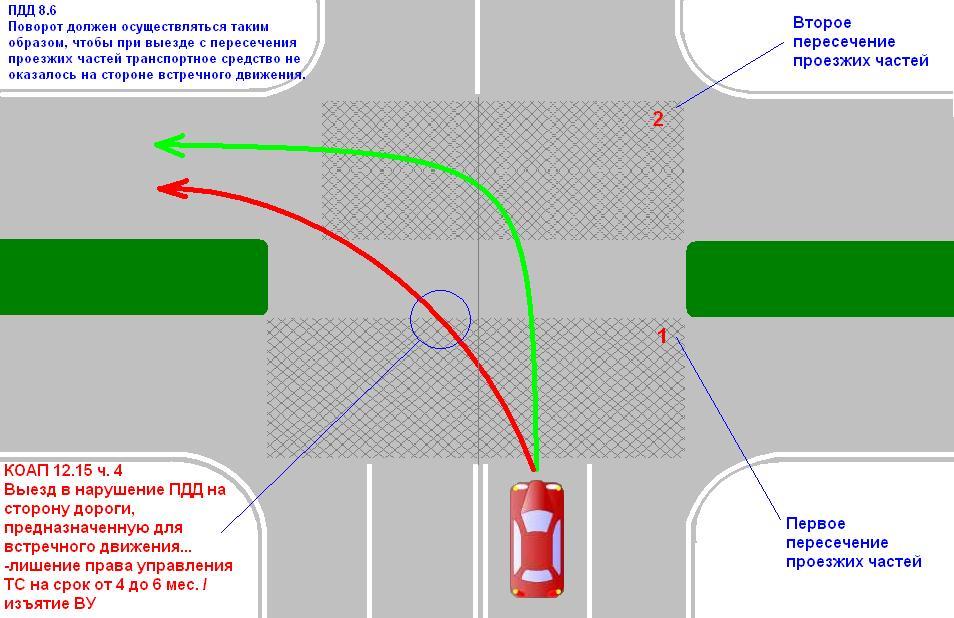 Точка на краю, где это происходит, является точкой изгиба.
Точка на краю, где это происходит, является точкой изгиба.
Пересечение — одно тело проходит через другое
Линия взаимопроникновения — край, где встречаются тела, это то, что мы пытаемся найти
Орфографические виды — Фасад, вид в плане или торец
Типовой экзаменационный вопрос
Всегда маркируйте свои точки — это значительно упрощает работу!
Приведенный ниже пример является обработанным примером из Graphics in Design & Communication, стр. 186
1 — Начертить план и фасад
|
2 — Вспомогательный вид или секущие плоскости? Вам нужно решить, будете ли вы использовать секущие плоскости или вспомогательный вид.
|
3 — Найти углы
|
4 — Поиск точек изгиба
|
5 — План
- Часто есть несколько точек, которые хорошо видны на виде сверху
- Найдите их и спроецируйте обратно на фасад
6 — Завершение
- точки изгиба, затем следуйте этой последовательности, чтобы завершить линии взаимопроникновения, включая скрытые линии.
- Может быть полезно использовать план, чтобы выяснить, что такое скрытая линия
Метод 1 — Пределы
|
3D-модели для рабочих примеров
|
p275 (красная книга), p177 (оранжевая книга) |
p178 (оранжевая книга) |
p179, (оранжевая книга) |
Метод 2 — Радиальные элементы
|
3D-модели рабочих примеров и вопросов
p188, Q4
Solidworks
eDrawings
Метод 3 — Горизонтальные или вертикальные плоскости сеченияЭти методы перечислены в вашем учебнике по отдельности, но идея у них одна и та же, поэтому здесь они рассматриваются вместе.
|
3D-модели обработанных примеров
Совет. Используйте функцию Плоскость сечения в Solidworks, чтобы быстро увидеть, как выглядят различные плоскости сечения.
p281 (красная книга), (оранжевая книга)
Solidworks
eDrawings
Метод 4 — Вспомогательные планыЭтот метод чаще всего используется в экзаменационных вопросах, поэтому убедитесь, что вы его знаете!
|
3D-модели рабочих примеров и вопросов
|
p186 (оранжевая книга) |
p190, q10 (оранжевая книга) |
Пересечение правильных тел — Геометрический чертеж
Последнее обновление Пн, 06 Мар 2023 |
Геометрический рисунок
Когда два тела проникают друг в друга, образуется линия пересечения. Иногда необходимо знать точную форму этой линии, обычно для того, чтобы можно было точно нарисовать одно или оба тела. В этой главе показаны линии пересечения, образующиеся, когда некоторые из более простых геометрических тел проникают друг в друга
Иногда необходимо знать точную форму этой линии, обычно для того, чтобы можно было точно нарисовать одно или оба тела. В этой главе показаны линии пересечения, образующиеся, когда некоторые из более простых геометрических тел проникают друг в друга
Два непохожих прямоугольных прлемы, сходящихся под прямым углом (Рис. 12/1)
ВЭ показывает, где углы 1 и 3 встречаются с большей призмой, и они проецируются на F.E. На плане показано, где встречаются углы 2 и 4 больший конец призмы проецируется до конечного элемента.
Две одинаковые квадратные призмы, встречающиеся под углом
На внешнем элементе показано, где углы 1 и 3 встречаются с большей призмой. На плане показано, где углы 2 и 4 встречаются с большим pdsm, и это спроецировано на FE 9.0010
3R0 УГЛОВАЯ ПРОЕКЦИЯ 2
1-Я УГЛОВАЯ ПРОЕКЦИЯ
3R0 УГЛОВАЯ ПРОЕКЦИЯ 2
1-Я УГЛОВАЯ ПРОЕКЦИЯ
3-Я УГЛОВАЯ ПРОЕКЦИЯ 6 3-Й УГОЛ ПРОЕКЦИЯ Шестиугольная призма с квадратной призмой справа
Две разные шестиугольные призмы, встречающиеся под углом (F»g.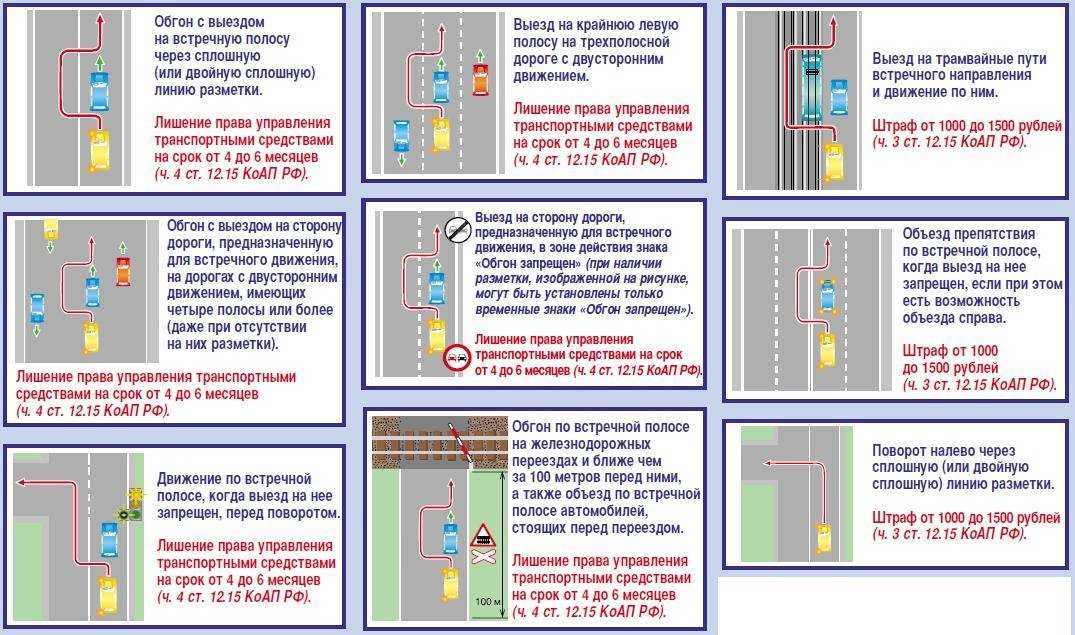 12/4)
12/4)
FE показывает, где углы 3 и 6 встречаются с большей призмой На плане показано, где углы 1, 2, 4 и 5 встречаются с большей призмой, и это проецируется до F E.
12/4
УГЛОВАЯ ПРОЕКЦИЯ
12/4
УГЛОВАЯ ПРОЕКЦИЯ
Шестиугольная призма, встречающаяся под углом с восьмиугольной призмой, центр которой не находится в одной вертикальной плоскости (Rg. 9040) FE показывает, где углы 3 и 6 встречаются с восьмиугольной призмой. На плане показано, где углы 1, 2, 4 и 5 встречаются с восьмиугольной призмой, и они проецируются вниз на Ft
Стороны шестиугольной призмы между углами 3-4 и 5-6 пересекаются с двумя сторонами восьмиугольной призмы. Изменение формы происходит в точках а и b. Положение a и b на FE (а затем поперек EE) находится путем проецирования вниз на FE через конец шестиугольной призмы (следуйте стрелкам). После этого перекресток на FE может быть завершен.
Квадратная призма, формирующая квадратную пирамиду в правом углу (рис. 12/6)
12/6)
Tha E.E. показывает, где углы 1 и 3 встречаются с пирамидой. Они проецируются на FE
. Углы 2 и 4 не так очевидны. На картинке показано, как эти углы встречаются с пирамидой, если пирамида была разрезана по X-X. получившееся сечение пирамиды было бы квадратным, а точки 2 и 4 лежали бы на этом квадрате. Не обязательно делать на чертеже полный, заштрихованный разрез, но необходимо нарисовать квадрат на плане. Поскольку точки 2 и 4 лежат на этом квадрате, найти их точное положение несложно. EE на план. Точки, где эти проекторы встречаются с квадратом, являются точными положениями пересечений углов 2 и 4 с пирамидой.
Квадратная пирамида и • шестиугольная призма встречаются
FE показывает, где углы 1 и 4 встречаются с пирамидой.
Углы 2 и А лежат в одной плоскости X-X. Если эту плоскость разбить на виде сверху пирамиды (по стрелкам), получится линия X-X-X. Углы 2 и 8 лежат в этой плоскости; их точное положение показано
. Углы 3 и 5 лежат в одной плоскости Y-Y.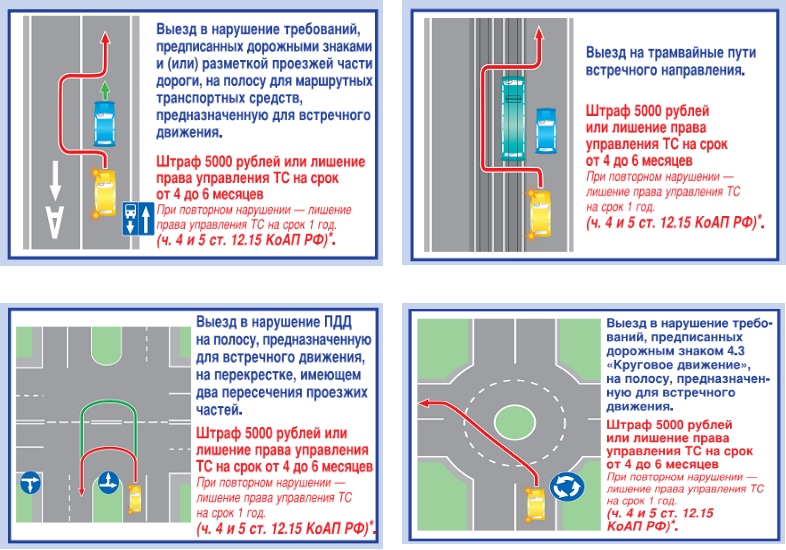 На виде сверху эта плоскость видна как зубец Y-Y-Y (следите за стрелками) Углы 3 и 5 лежат на этой плоскости; их точное положение показано.
На виде сверху эта плоскость видна как зубец Y-Y-Y (следите за стрелками) Углы 3 и 5 лежат на этой плоскости; их точное положение показано.
Два одинаковых цилиндра, «встречающихся под прямым углом» (Рис. 12/8)
Меньший цилиндр разделен на 12 равных секторов на ИП и в плане (ЭЭ показывает, как они расположены вокруг цилиндра) .
На плане показано, где три сектора встречаются с большим цилиндром, и эти пересечения проецируются вниз на прямую прямую, чтобы соответствовать соответствующему сектору на высоте 12 дюймов 3 фута и т. д.
)7
[С? 1
Два непохожих цилиндра, встречающихся под углом (Рис. 12/9)
Метод идентичен методу последней задачи. Меньший цилиндр разделен на 12 равных секторов на FE и на плане
. На плане показано, где эти сектора встречаются с большим цилиндром, и эти пересечения проецируются до FE, чтобы соответствовать соответствующим секторам в 1 *. 2′. 3\ и т. д.
2′. 3\ и т. д.
Два неодинаковых цилиндра, сходящиеся под углом, центры которых не лежат в одной вертикальной плоскости (рис. 12/10)
Опять же, метод идентичен предыдущему примеру. Меньший цилиндр разделен на 12 равных секторов на FE и на плане
. План показывает, где секторы встречаются с большим цилиндром, и эти пересечения проецируются вниз на FE, чтобы соответствовать их соответствующим секторам в 1 ‘. 2′, 3’. и т. д.
Цилиндр, встречающийся с квадратной пирамидой под прямым углом
FE показывает, где точки 1 и 7 встречаются с пирамидой, и они проецируются на план.
Рассмотрим положение точки 2. Поскольку цилиндр и пирамида проникают друг в друга, точка 2 лежит и на цилиндре, и на пирамиде. Его положение на цилиндре видно довольно легко. На FE он лежит на линии, обозначенной 2.12, а на плане — на линии, отмеченной 2.6. Его положение на пирамиде не столь очевидно. Представьте, что на ФЭ удалена часть пирамиды, которая находится выше линии 2. 12. Полученное сечение пирамиды будет квадратом, а точка 2 будет располагаться где-то по периметру этого квадрата. Нет необходимости строить полное заштрихованное сечение пирамиды по линии 2.12, но квадрат, который получится участок строится по плану. На рис. 12/11 он отмечен как «SQ 2.12». Так как точка 2 лежит где-то на линии 2.6 (в плане), то ее точное положение находится на пересечении квадрата и линии. На плане это обозначено цифрой 2′.
12. Полученное сечение пирамиды будет квадратом, а точка 2 будет располагаться где-то по периметру этого квадрата. Нет необходимости строить полное заштрихованное сечение пирамиды по линии 2.12, но квадрат, который получится участок строится по плану. На рис. 12/11 он отмечен как «SQ 2.12». Так как точка 2 лежит где-то на линии 2.6 (в плане), то ее точное положение находится на пересечении квадрата и линии. На плане это обозначено цифрой 2′.
Точка 12′ — пересечение того же квадрата и линии 8.12 (в плане).
Процесс Тиа повторяется для каждой точки по очереди. Когда пересечение будет завершено в плане, несложно спроецировать точки вверх на конец конечного элемента, нарисовав там пересечение.
1-Я УГЛОВАЯ ПРОЕКЦИЯ
- Рис. 12/11
1-Я УГЛОВАЯ ПРОЕКЦИЯ
Цилиндр, встречающийся под углом с квадратной пирамидой (Рис. 12/12)
FE показывает, где точки 1 и 7 встречаются с пирамидой, и они проецируются на план.
Рассмотрим положение точки 2. На FE она лежит где-то вдоль линии, отмеченной 2.12, а в плане она лежит на линии, отмеченной 6.2. Если та часть пирамиды над чертой. 2.12 в КЭ убрали, точка 2 лежала бы на периметре получившегося сечения. Этот периметр можно провести на плане и . на рис. 12/12 она показана как линия, отмеченная как «РАЗДЕЛ 2.12». Точка 2 должна лежать на этой линии: она также должна лежать на линии, отмеченной 6.2, и ее точное положение — это пересечение этих двух линий.
На FE она лежит где-то вдоль линии, отмеченной 2.12, а в плане она лежит на линии, отмеченной 6.2. Если та часть пирамиды над чертой. 2.12 в КЭ убрали, точка 2 лежала бы на периметре получившегося сечения. Этот периметр можно провести на плане и . на рис. 12/12 она показана как линия, отмеченная как «РАЗДЕЛ 2.12». Точка 2 должна лежать на этой линии: она также должна лежать на линии, отмеченной 6.2, и ее точное положение — это пересечение этих двух линий.
Точка 12′ является пересечением той же линии сечения и линии, обозначенной 8.12.
Этот процесс повторяется для каждой точки по очереди. Когда план готов, пересечение можно спроецировать на два других вида. Для ясности эти проекции не показаны.
1-Й УГОЛ
Цилиндр, встречающийся под углом с шестиугольной пирамидой
Еще раз на плане начерчены линии, которые представляют собой периметры секций, взятых на КЭ по линиям 1; 2. 12; 3. 11. etc Все линии построения на рис. 12/13 предназначены для нахождения периметров этих сечений.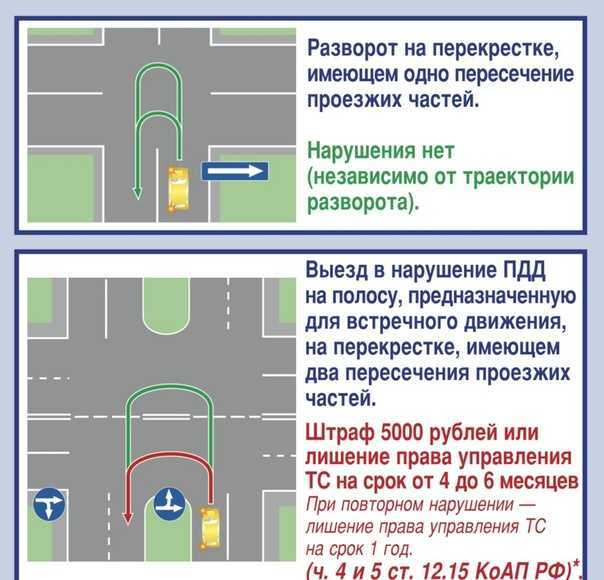
Линия мтерпенового нетто-рациона. первой нарисованной на плане является пересечение линии 1.7 с сечением 1. линии 2.6 с сечением 2.12 (указывается точка 2*). строка 3.5 с разделом 3.11 (указывается точка 3*), строка 4 с разделом 4.10. и т. д.
Когда пересечение выполнено на плане, его можно спроецировать на два других фасада. Для удобства эти проекции не показаны
Цилиндр, встречающийся с конусом, конус, огибающий цилиндр (рис. 12 /14)
Цилиндр разделен на 12 равных секторов» на Ф.Э. и на плане.
Рассмотрим точку 2. На FE она лежит где-то вдоль линии, отмеченной 2.12, а на плане она лежит на линии, отмеченной 2.6. Если. на КЭ.. та часть конуса, которая выше линии 2.12, была удалена, точка 2 лежала бы где-то на периметре получившегося сечения. В этом случае сечение конуса представляет собой круг, и радиус этого круга легко проецируется на план. На рис. 12/14 участок отмечен на плане как «РАЗДЕЛ 2.12», а точное положение точки 2 — это пересечение этого участка и линии, отмеченной 2. 6. Точка 12′ является пересечением того же сечения и линии, отмеченной 12,8
6. Точка 12′ является пересечением того же сечения и линии, отмеченной 12,8
Этот процесс повторяется для каждой точки по очереди. Когда план завершен, точки можно спроецировать на FE; это не показано для cianty.
Цилиндр и конус.
Построения точно такие же, как и в предыдущем примере с одним дополнением tmail
EE показывает точку касания между цилиндром и конусом. план, как показано
Цилиндр и конус, «цилиндр, охватывающий конус» (Рис. 12/16)
Требуемая здесь конструкция представляет собой модифицированную версию двух предыдущих. Вместо деления цилиндра на 12 равных секторов, некоторые из которых не будут использоваться, на EE выбирают несколько точек. Они отмечены в верхней части цилиндра как a. б и в, в то время как нижняя чаша отмечена 1.2.3 конец 4.
Как и прежде, сечения конуса поперек каждой из этих точек проецируются на план от ВЭ. Затем каждая точка защищена от ВЭ для удовлетворения соответствующий ему участок на плане в точках а’, б’. с*. 1′. 2′, 3″ и 4\
с*. 1′. 2′, 3″ и 4\
Затем эти точки защищены вплоть до FE. Для ясности это не показано.
I 1-Й РАКУРС
ПРОЕКЦИЯ
I 1-Й РАКУРС
Рис. план.
Разрезы проецируются на план из КЭ. Плоскости разрезов находятся на одном уровне с линиями 1 ; 2,12; 3.11; 4.10. и т. д., и эти сечения появляются на плане в виде кружков.
На плане сектора цилиндров спроецированы поперек, чтобы соответствовать их соответствующему сечению на высоте 1 2 фута. 3*. 4′ и т. д.
Когда взаимопроникновение завершено на плане, его можно спроецировать до FE. Для ясности эта конструкция не показана.
Рис. 12/18
Цилиндр, встречающийся с конусом, центры которого не лежат в одной вертикальной плоскости (Рис. 12/17) Разделить цилиндр на 12 равных секторов на ПП и в плане
Сечения проецируются от КЭ до плана, плоскости разреза на уровне линий 1; 2,12; 3.11; 4.10. и т. д. Эти участки отображаются на плане в виде кругов. На плане сектора от цилиндра ограждены поперек до пересечения с соответствующим им сечением в точках 1′. 2*. 3′. и т. д. Тогда полное взаимопроникновение может быть спроецировано на FE. эта конструкция не показана.
2*. 3′. и т. д. Тогда полное взаимопроникновение может быть спроецировано на FE. эта конструкция не показана.
1-Я УГЛОВАЯ ПРОЕКЦИЯ
Рис. 12/17
Цилиндр, встречающийся с полусферой (Рис. 12/19) Решение точно такое же, как в последнем примере, за исключением того, что сечения проецируются на восточноевропейское направление, а не на план.
КРУГЛЫЕ КРИВЫЕ Внезапное изменение формы любого несущего компонента приводит к возникновению центра напряжения, т.е. область, которая подвергается более высоким нагрузкам, чем остальная часть компонента, и, следовательно, более подвержена разрушению под нагрузкой. Чтобы избежать этих острых углов, используются радиусы наполнителя. Эти радиусы позволяют распределять нагрузку более равномерно, делая компонент более прочным
1-Я УГЛОВАЯ ПРОЕКЦИЯ
РАДИУС СКЛАДКИ
1-Я УГЛОВАЯ ПРОЕКЦИЯ
РАДИУС СКЛАДКИ
- Рис. радиусы удаляются, и получается кривая пересечения. На рис. 12/20 показан пример этого.

Разрезы обозначены на КЭ. На плане они обозначены кружками. Точки, в которых эти секции «выходят за рамки плана», можно легко увидеть (на 1, 2, 3 и 4), и они проецируются на FE, чтобы показать соответствующие секции
ПРОЕКЦИЯ НА 3-Й УГОЛ
На рис. 12/21 показано, как можно использовать радиус скругления на конце накидного ключа линии секций не показаны). Точки, в которых эти сечения выходят за пределы плана, легко увидеть, и эти точки (1, 2, 3, 4 и т. д.) проецируются вниз на FE, чтобы соответствовать соответствующим сечениям на 12′. 3″. A’ и т. д.
3-Й УГОЛ ПРОЕКЦИИ
Рис. 12/21
Чтобы найти истинную длину линии e, которая не параллельна ни одной из главных плоскостей, и найти угол, который линия образует с F.V.P. (Рис. 13/2) Это линия AB. На Ф.В.П. он виден как ab и на H Pas a,6,.
Один конец линии A остается неподвижным, в то время как B поворачивается так, чтобы AB был параллелен H P. B теперь находится в B’ и на F.V.P. b теперь находится в b’.
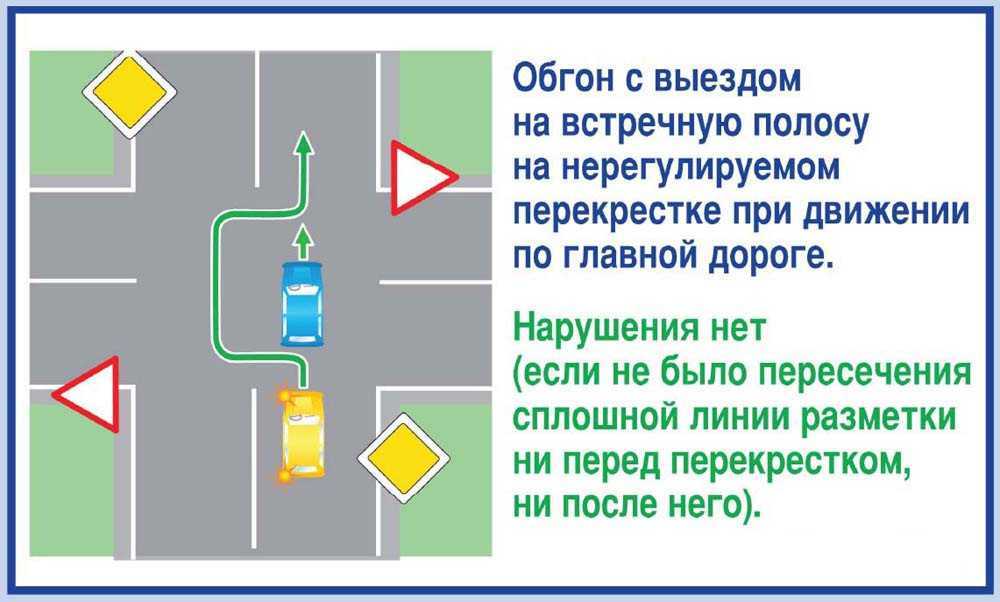 Так как линия параллельна H.P. он проецирует свою истинную длину на Н.П. Это показано как axbt. Обратите внимание, что b и b находятся на одинаковом расстоянии от линии XY.
Так как линия параллельна H.P. он проецирует свою истинную длину на Н.П. Это показано как axbt. Обратите внимание, что b и b находятся на одинаковом расстоянии от линии XY. Поскольку AB’ (и ab’) параллельны H P., угол, который AB образует с F.V.P. может быть измерено Это показано как 0.
НАЧАЛЬНЫЕ УСЛОВИЯ (ABIS НЕ ПАРАЛЛЕЛЬНО НИ ОДНОЙ ПЛОСКОСТИ)
ENO A СОХРАНЯЕТСЯ СТАЦИОНАРНО, А B ПОВЕРНУТ ТАК, ЧТО AB БУДЕТ ПАРАЛЛЕЛЬНО H.R ИСТИННАЯ ДЛИНА НА KP ОТ УГЛА, КОТОРЫЙ СОСТАВЛЯЕТ ЛИНИЯ С F.V.P. на любой из основных планов и найти англу, что линия mekei с Е.П. (Рис. 13/3) Это линия AB. На Ф.В.П. ¡t отображается как ab и на H.P. как*./»,.
Один конец линии B остается неподвижным, в то время как A поворачивается так, чтобы AB был параллелен F.V.P. А теперь в А’ и. на HP.. a теперь в #’. Поскольку колено теперь параллельно F.V.P. он проецирует свою истинную длину на FVP. Это показано как «¿r. Обратите внимание, что a и o находятся на одинаковом расстоянии от линии XY.

Поскольку BA- (и b,a’) параллельны F.V.P., угол, который AB образует с H.P. можно моурировать. Это показано как
- ПРОЕКЦИЯ 1-Й КОЛЕСО
ДЛИНА AE
ИСТИННАЯ ДЛИНА ИСТИННАЯ ДЛИНА
Рис. 13/4 представляет собой пример применения теории, показанной выше. Он показывает, насколько просто применить эту теорию.
Пилон поддерживается тремя тросами. Дан план и возвышение хевсеров. Найдите их истинную длину и угол, который они образуют с землей.
На плане каждый трос поворачивается до параллели с F.V.P. Новые положения концов тросов проецируются до конца F.E., соединенного с пилоном в конце A и B. Это дает истинные длины и углы.
ИСТИННАЯ ДЛИНА ИСТИННАЯ ДЛИНА
ДЛИНА AE
Чтобы найти следы прямой линии по плану и высоте этой линии (Рис. 13/6) Линия AB. Если линия получится, то она будет проходить через обе плоскости, давая следы Т. и Тн.
»b выпускается по линии XY. Это пересечение проецируется вниз, чтобы встретиться с a ,b, произведенным в T*.

»b выпускается по линии XY. Это пересечение проецируется вниз, чтобы встретиться с a ,b, произведенным в T*.
Начертить алаватлон и план Уны АВ, учитывая ее* истинную длину и расстояния концов линии от основных плоскостей, в данном случае а и
1. Зафиксировать точки а и а на заданных расстояниях av и а» от линии XY. Они измеряются на общем перпендикуляре к XY.
2. Проведите линию, параллельную XY, на расстоянии b от XY.
3. С центром a. радиус равен истинной длине AB. d’aw дугу, чтобы разрезать линию, проведенную параллельно XY в точке C.
4. Из a провести линию, параллельную XY, до пересечения с линией из C, проведенной перпендикулярно XY в точке 0.
5. Начертить прямую, параллельную XY к ХУ. расстояние b» от XY.
6. С центром *„ радиусом a.D нарисуйте дугу, чтобы разрезать линию, проведенную параллельно XY в b,.
7. Проведите линию от точки b перпендикулярно XY до пересечения с линией, проведенной параллельно XY через точку C в точке b sb — высота линии, a J> — план линии.

Для построения плана линии АВ по натяжению одного конца линии от линии XY в плане (а«), истинной длине линии и высоте (рис. 13/7)
1 , Из b провести линию, параллельную линии XY
2. С центром a, радиус равен истинной длине линии AB. начертите угол, чтобы разрезать параллельную линию в C.
3. Из a, (дано), проведите линию, параллельную линии XY, до пересечения с линией, проведенной из C перпендикулярно XY в D
4. С центром *, . радиусом, равным *,D, нарисуйте дугу, чтобы встретиться с линией, проведенной из b перпендикулярно XY в b,.
ПРОЕКЦИЯ НА 3-Й УГОЛ
ПРОЕКЦИЯ НА 3-Й УГОЛ
> 0
— 9″-■J
1 J
3-Я УГЛОВАЯ ПРОЕКЦИЯ
3-Я УГЛОВАЯ ПРОЕКЦИЯ
1-Я УГЛОВАЯ ПРОЕКЦИЯ
3R0 УГЛОВАЯ ПРОЕКЦИЯ 901 60016
906 19 1-Й УГОЛ ПРОЕКЦИЯ
ДАННЫЙ
УГОЛ Рис. 13/9
Рис. 13/10
АЛЬТЕРНАТИВНОЕ РЕШЕНИЕ
Y СЛЕДЫ ПЛОСКОСТИ
1-Я УГЛОВАЯ ПРОЕКЦИЯ
Построение возвышения линии AB по плану линии и угла, образующего линию с горизонтальной плоскостью (Рис. 1). 9)
1). 9)
1. Начертите план и от него и проведите перпендикуляр
2. От другого конца плана проведите линию под углом, данным для пересечения перпендикуляра в С.
3. Оттуда проведите перпендикуляр в XY, чтобы встретиться с XY в b. 4 Из a проведите линию, перпендикулярную XY, и отметьте
XY до* равной a.c ab ia требуемой высоты.
УГОЛ Рис. 13/9
3R0 УГОЛ ПРОЕКЦИЯ
ДАННЫЙ
Рис. 13/10
АЛЬТЕРНАТИВНОЕ РЕШЕНИЕ
Начертить участок линии AB, учитывая высоту линии и угол, который линия образует с вертикальной плоскостью Icel ( Рис. 13/10)
Эта конструкция очень похожа на предыдущую и можно следовать из инструкций, данных для этого примера.
Y СЛЕДЫ ПЛОСКОСТИ
НАКЛОННАЯ ПЛОСКОСТЬ
Определение
Наклонная плоскость наклонена к двум главным плоскостям и перпендикулярна третьей.
На рис. 13/11 показана прямоугольная плоскость, обращенная к валу высокого давления. закончить E.V. P. конец перпендикулярен F.V.P. Поскольку он перпендикулярен F.V.P., истинный угол между наклонной плоскостью и H P. можно измерить на F.V.P. Это угол 4-
P. конец перпендикулярен F.V.P. Поскольку он перпендикулярен F.V.P., истинный угол между наклонной плоскостью и H P. можно измерить на F.V.P. Это угол 4-
ПРОЕКЦИЯ ПЛОСКОСТИ Рис. 13/11
ПРОЕКЦИЯ ПЛОСКОСТИ
На верхнем рисунке показаны следы плоскости после скрепления. На нижнем рисунке показана полная проекция самолета. Должно быть очевидно, как получается полная проекция, если вам даны следы и сказано, что плоскость прямоугольная
На рис. 13/12 показано треугольное фортепиано, наклоненное к F.V.P. и E.V.P.. и перпендикулярно H.P. Поскольку он перпендикулярен к H.P., истинный угол между наклонной плоскостью и F.V.P. можно измерить на л.с. Этот угол равен $.
ПРОЕКЦИЯ НА 3-Й УГОЛ
Еще раз должно быть очевидно, как получить полную проекцию наклонной плоскости, если вам даны следы и сказано, что плоскость треугольная.
СЛЕДЫ САМОЛЕТА m*
Рис. 13/12
ПРОЕКЦИЯ ПЛОСКОСТИ
Чтобы найти истинную форму наклонной плоскости Если наклонную плоскость повернуть так, чтобы она была параллельна одной из базовых плоскостей, истинная форма может быть защищена. 13. план самолета. HT, поворачивается к HT. Истинную форму самолета потом можно нарисовать на Ф В.П.
13. план самолета. HT, поворачивается к HT. Истинную форму самолета потом можно нарисовать на Ф В.П.
3-Я УГЛОВАЯ ПРОЕКЦИЯ
СЛЕДЫ ПЛОСКОСТИ
Рис. 13/15
Рис.0046 СТОРОНА A
Рис. который наклонен ко всем трем основным плоскостям.
3-Й УГОЛ ПРОЕКЦИИ
Рис. 13/14
Рис. 13/14 показывает пример. На основании стоит косая, усеченная, прямоугольная пирамида. Задача состоит в том, чтобы найти истинную форму сторон A и B
В FE сторона A поворачивается вертикально, и ее вертикальная высота проецируется на EE, где можно нарисовать истинную форму стороны A. 3. На рис. имеет истинную длину 100 мм. Конец Б линии находится на 12 мм впереди В П.; конец А находится также «n перед ВП. Начертите план и высоту этой линии, определите и укажите ее В.Т и В.Т. Измерьте, укажите и укажите угол наклона линии к В.П. Совместная приемная комиссия
Рис. 3
Рис. 3
РАЗМЕРЫ В мм
РАЗМЕРЫ В мм
4. Линия AB истинной длины 88 мм лежит во вспомогательной вертикальной плоскости, которая составляет с вертикальной плоскостью угол 30°. Линия наклонена под углом 45° к горизонтали, точка В является самой нижней на расстоянии 12 мм по вертикали от горизонтальной плоскости и 12 мм впереди от вертикальной плоскости Нарисуйте план и высоту АВ и четко обозначьте их на чертеже. Ассоциированная экзаменационная комиссия
Линия наклонена под углом 45° к горизонтали, точка В является самой нижней на расстоянии 12 мм по вертикали от горизонтальной плоскости и 12 мм впереди от вертикальной плоскости Нарисуйте план и высоту АВ и четко обозначьте их на чертеже. Ассоциированная экзаменационная комиссия
7. Проекции связки RST показаны на рис. 6. Определите истинную форму связки. Ассоциированная экзаменационная комиссия
:. План и высота двух прямых даны на рис. 7. Найдите истинные длины линий, истинный угол между ними и расстояние между А и С
Объединенный совет южных университетов
5. План линии Длина 82 мм показана на рис. 4. Высота одного конца находится в точке b’. Завершите возвышение и измерьте наклоны лба к Н. П. и В. П.
Школьные экзамены Лондонского университета
|
и |
|||
|
ф |
Рис. 4 РАЗМЕРЫ Н мм 6. На рис. 5 показан план конца А линии АВ. I На рис. 8 показан план и вид треугольной пластинки. Нарисуйте эти два вида и. найдя истинную длину каждой стороны, нарисуйте истинную форму пластинки. Измерьте и укажите три угла с точностью до градусов. Экзаменационная комиссия школ Оксфорда и Кембриджа Рис. 8 Рис. 8 РАЗМЕРЫ В мм РАЗМЕРЫ В мм 10. На рис. 9 показаны вид и план треугольника ABC. Определить истинную форму и размер треугольника University of L on Don Школьные экзамены 11. На рис. 10 показаны два вида косой треугольной пирамиды, стоящей на своем основании. Изобразите данный вид вместе со вспомогательным видом, смотрящим в направлении стрелки А, перпендикулярной ВС. Нарисуйте также истинные формы сторон пирамиды. пирамида. |
 Он появился как короткий и длинный вопрос.
Он появился как короткий и длинный вопрос.  Часто это можно сделать с обоими, но вспомогательные хорошо работают, если есть призма под углом. Шаги ниже предназначены для вспомогательного вида.
Часто это можно сделать с обоими, но вспомогательные хорошо работают, если есть призма под углом. Шаги ниже предназначены для вспомогательного вида. 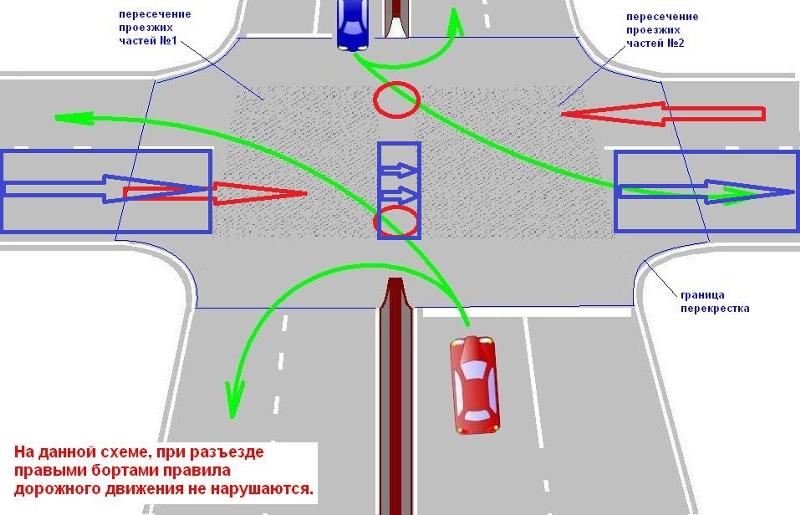 Найдите, найдя, где линия проекции пересекает ребро, на котором находится точка. В этом примере
Найдите, найдя, где линия проекции пересекает ребро, на котором находится точка. В этом примере  е. 1), конец (т.е. 4) и точки изгиба (т.е. s), мы можем найти линии.
е. 1), конец (т.е. 4) и точки изгиба (т.е. s), мы можем найти линии. 
 Плоскости сечения будут создавать простые формы, такие как тела или прямоугольники для этих объектов.
Плоскости сечения будут создавать простые формы, такие как тела или прямоугольники для этих объектов. 
 Конец A находится в плоскости H.T.V. Конец B находится в H P. Прямая AB перпендикулярна плоскости H.T.V. Начертите план и фасад AB. Совместная комиссия по зачислению (H.V.T. = горизонтальные конечные вертикальные дорожки)
Конец A находится в плоскости H.T.V. Конец B находится в H P. Прямая AB перпендикулярна плоскости H.T.V. Начертите план и фасад AB. Совместная комиссия по зачислению (H.V.T. = горизонтальные конечные вертикальные дорожки) 