Значок десятки
Как пишется знак больше и знак меньше
 Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и "вспомнить" в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
- Как пишется знак больше
- Как пишется знак меньше
- Знак "больше или равно"/«меньше или равно" (как набрать на клавиатуре)
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова "погуглить", а сейчас просто нужен ответ на вопрос "в какую сторону писать знак", тогда для вас мы приготовили краткий ответ - знаки больше и меньше пишутся так, как показано на изображении ниже.
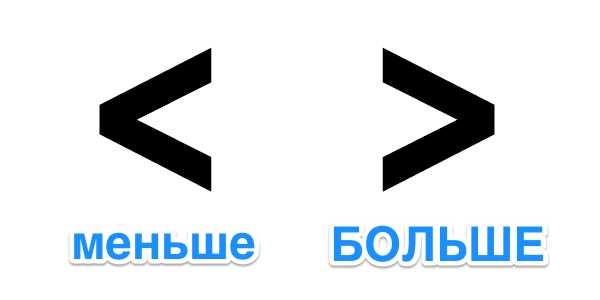
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше

В общем и целом логика понимания очень проста - какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону - такой и знак. Соответственно, знак больше влево смотрит широкой стороной - большей.
Пример использования знака больше:
- 50>10 - число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
 Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной - меньшей, то перед вами знак меньше.Пример использования знака меньше:
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной - меньшей, то перед вами знак меньше.Пример использования знака меньше:
- 100<500 - число 100 меньше числа пятьсот;
- на заседание явилось <50% депутатов.
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знак больше или равно/меньше или равно
Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак "меньше или равно" или знак "больше или равно".
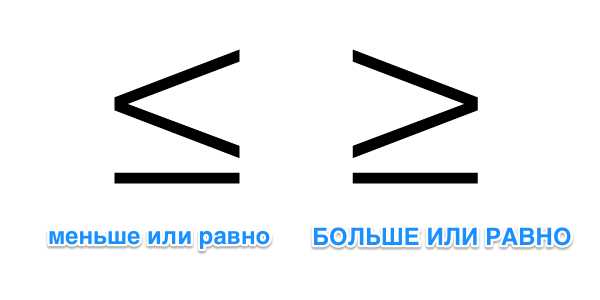
Однако относительно этих знаков у некоторых возникает другой вопрос - как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, "больше или равно" обозначая как ">=", что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки "≤" и "≥" выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать "больше или равно" на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов - просто поставьте знак больше с зажатой клавишей "alt". Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
alt+ю
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
≥
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать "меньше или равно" на клавиатуре вы можете по аналогии со знаком больше - просто поставьте знак меньше с зажатой клавишей "alt". Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
alt+б
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
≤
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу - всё просто.
© OchProsto.com
ochprosto.com
Символика числа 10 (десять)
Тетраксис Пифагора — десять точек — символ, открывающий тайну универсальной природы. Тетраксис (1 + 2 + 3 + 4 = 10) символизирует божественное; единица означает точку, двойка — протяженность, тройка (треугольник) — плоскость, четверка — объем, или пространство.
На Древе Жизни находятся десять сфер (сeфирот). Четыре буквы священного имени Бога, расположенные в форме треугольника, дают число десять (тетраграмматон). Кроме того, десятка — это сумма девятки как числа окружности и единицы-центра, отсюда ее значение совершенства. Это символизируется также столбом, вокруг которого водят хоровод. Единица-начало, по учению каббалистов, есть также Единица-конец существ и вещей, а вечность, с этой точки зрения, есть только вечное настоящее. Поэтому древние символисты изобразили эту идею точкой в центре круга: Единица-начало (точка) в центре вечности (круг — линия без начала и конца). Эта мысль выражена в числе десять: «Это образ того, как Бог создал мир: из ноля Он, благодаря действию единицы, сотворил все живое, и это есть десятка». Число десять, состоящее из цифр 1 и 0, символизирует любовь к Богу и ближнему, силу, единство мироздания (как две пятерки), итог Божественного создания, выражаемого двумя противоположными началами: мужским и женским, светом и тьмой, землей и небом; оно представляет собой дух и материю. Из небытия, космического хаоса 0, рождается жизнь — 1.
Число десять можно толковать и следующим образом: 1 — это Бог; 0 — бесконечность. Качества цифры 1 даруют честь, веру, уверенность в себе, имя и славу, действующие в соответствии с законом Божественного предопределения; 0 подталкивает к духовной борьбе, которая приводит человека к пониманию своего предназначения в этой жизни. Число в этом аспекте понимается как выражающее сакральное единство материального и духовного начал: число десять — само совершенство, так как обладает обоими началами. Если его начертить так, как на рисунке, это индуистский лингам, символ, подобный Соломоновой печати (переплетенным треугольникам — мужскому и женскому). Лингам считается священным символом Шивы; в ритуальной практике индуизма это изображение широко распространено и исполнено глубокого смысла.
Китайцы десятку изображают в виде равностороннего креста, центр которого образован иероглифом «чи», что символизирует человеческое «Я», перед которым лежат оба пути, инь и ян. Это совершенная фигура, символ равновесия и гармонии.
Десять — венец творения. Именно десятка почитается как наиболее сакральное и полное число, поскольку оно представляет (отражает) возвращение от единицы к изначальной пустоте. Десятка содержит все числа, а следовательно, все вещи и возможности, это основа и поворотный пункт всего счета. Означает нечто всеобъемлющее, закон, порядок, власть. Это число успеха, оно символизирует осуществление.
Десятка содержит все числа, а следовательно, все вещи и возможности, это основа и поворотный пункт всего счета. Означает нечто всеобъемлющее, закон, порядок, власть. Это число успеха, оно символизирует осуществление.
Это также символ красоты, Высшей гармонии, совершенное число Космоса. Число десять символизирует общую идею изобилия, неограниченного количества, законченности. Оно также связано с устанавливаемым человеком порядком: пять пальцев левой руки представляют царство Закона, а пять пальцев правой пуки — царство Силы. У пифагорейцев десятка — это монада, возобновление ряда, бесконечное распространение, совершенство.
В Риме это число изображалось знаком «X» — совершенной фигурой, означающей полноту. Десятка — это также число завершения путешествий и возвращения в исходную точку. Одиссей странствовал девять лет, а на десятый год вернулся. Троя была в осаде девять лет и на десятый год пала.
В Каббале десять — это числовое значение буквы («йод» — вечного слова), первой буквы имени Бога. Символизирует блестящую способность к пониманию, божественную поддержку, Десятикнижие, Царство, десять имен Бога, число сeфирот, обычно изображаемых как Древо Жизни. Первая их них является монадой и первопричиной остальных девяти, образующих три троицы, каждая из которых есть образ первоначальной Троицы (мужское, женское и объединяющее их понимание). Десятая, Адонай, символизирует мистическое возвращение к единству. В храме Соломона было десять умывальниц, столов и подсвечников. Херувимы были десять локтей высотой. Десять левитов правили до потопа.
Единица в каббалистике рассматривается также как сумма всех возможностей, причем все сотворенные существа являются только ее составными частями; таким же образом Единица-Человек образована суммой миллионов клеточек, составляющих его существо.
В шумеро-семитской традиции десятый день празднования весны отмечался процессией, изображающей всех богов. В Библии Господь дает человечеству десять заповедей. Это законы нравственного мирового порядка, поддерживающие взаимоотношения людей и определяющие нормы их сосуществования.У христиан существуют притчи о десяти лампадах, девах, талантах. Богу посвящалась десятина. В исламе большую роль играет десятина.Степени десятки — 100 и 1000 — лежат в основе всей индуистской космологии.В тантрических текстах десять — число лепестков чакры Свадхистана.В Китае — это Десять Тысяч Вещей, то есть неисчислимое, символизирующее все совокупность явлений. Десять Небесных Стеблей (Гань), возможно, связаны с десятидневной неделей наиболее распространенного китайского цикла.(Источник)
Тройственный символизм десятки и её графическое изображение. Эзотерический смысл числа десять состоит в том, что оно продолжая линию, намеченную числом девять, символизирует идею абсолютного совершенства и числовой завершенности, возвращающей к источнику всех однозначных чисел — единице. Корнелий Агриппа говорил на этот счёт: "Число десять названо всемирным и полным числом, означающим полный путь жизни, ибо от этого числа считают повторениями, и оно содержит в себе все числа или объясняет их своими, помножая их. Поэтому его считают числом различных энергий… Нет числа выше его и все "десятое имеет нечто божественное"". В этом, только что названном, божественном аспекте число десять означает небо, высшую целостность, абсолютную полноту, возврат к единству на новом уровне. В своем природном аспекте десятка символизирует проявленную природу, материю, выполняющую небесную волю и верховный закон. В своем человеческом аспекте число десять символизирует то, что может быть названо Богочеловечеством, реализующим принцип Царства Божия на земле, или еще точнее Богочеловеком, Небесным Человеком или Адамом Кадмоном. Графическим изображением десятки будет также крут (окружность плюс её центр), змея, ползущая по столбу (движение плюс покой, замысел плюс форма), а также Древо Сефирот.
Атрибуты и сущность десятки Выступая как число абсолютной полноты и тотальной завершенности, десятка представляет собой синтез бытия и небытия. По мнению Дебаролля "знак десяти составлен из единицы, означающей бытие, и нуля, выражающегo небытие: оно, стало быть, содержит дух и материю; оно есть высшая точка разума человечества, которое все исчисляет им". Многие оккультные философы (Корнелий Агриппа, Сен-Мартин, Элифас Леви) считали, что десятка своим совершенством способна исправить другие несовершенные, неполные, разделенные друг с другом числа. Сен-Мартин писал: "Число соединенное в декаду никогда не представляет образа расчленения и бесформенности. Даже 2 и 5, разделяющие декаду, дурны только тогда, когда они уединены. Соединенные в десяток они теряют свой дурной и бесформенный характер". Сходную характеристику дает числу 10 Блаватская: "Десять или Декада приводит все эти единицы назад к единству и заканчивает таблицу Пифагора. Потому эта фигура — единица в нуле — была символом Божества Вселенной и Человека. Таков тайный смысл "мощного захвата львиною лапою племени Иуды" ("пожатие мастера-масона") между двумя руками, соединенные пальцы дают число десять".
Мэнли Холл также подчеркивает завершающий и объединяющий аспект числа 10: "Декада, 10, согласно пифагорейцам, есть величайшее число не только потому, что это тетрактис (10 точек), но и потому, что она объемлет все арифметические и гармонические пропорции. Пифагор говорит, что 10 есть природа числа, потому что все народы приходят к ней, и когда они приходят к ней, они возвращаются к монаде. Декада называлась и небом, и миром, потому что первое включает второе. Будучи универсальным числом, декада прилагалась пифагорейцами к тем вещам, которые характеризуются возрастом, силой, верой, необходимостью, мощью памяти. Она также называлась неутомимой, потому что, подобно Богу, она не подвержена усталости. Пифагорейцы делили небесные тела на десять порядков. Они также утверждали, что декада совершенствует все числа и объемлет в своей природе чётные и нечетные, подвижные и неподвижные, добрые и злые. Они ассоциировали её силу со следующими божествами: Атласом, потому что он несет числа на своих плечах, Уранией, Мнемозиной, Солнцем, планетами и Единым Богом."
Число 10, составленное из суммы первых четырёх чисел натурального ряда (1+2+3+4=10), вбирает в себя всю вселенную и представляет собой четырехликое единство бытия в Идеальном Аспекте, Мистическим Квадратом, вписанным в окружность. X. Э. Керлот дает десятке следующую характеристику:
"Десять в десятеричной системе символизирует возвращение к единице. В тетрактисе (пифагорейском треугольнике, где точки в четырёх убывающих рядах — четыре, три, два, один — суммируются до десяти) оно относится к четырём. Символизируется также духовное достижение, равно как и единство его функций в качестве чётного (или амбивалентного) числа или в качестве начала новой, сложной серии чисел. Согласно некоторым теориям, десять символизирует целостность универсума (в двух планах: метафизическом и материальном), т. к. оно приводит все к единству. Известно истолкование этого числа как совершенства: эта традиция, берущая начало в древневосточном и через пифагорейскую школу приводящая к Св. Иерониму."
Десятка изображается не только неподвижным статическим символом Древа Сефирот, но и вполне подвижной фигурой «денера». В определенном смысле она есть вращающийся круг. Рене Генон считает, что наилучшим графическим символом десятки будет круг, разделенный на четыре равные части посредством креста, образованного двумя прямоугольными диаметрами. Если квартинер геометрически в статическом аспекте может быть изображен в виде квадрата, то в динамическом аспекте, он изображен как подвижный, вращающийся вокруг своего центра крест. Такой денер, то есть полный числовой цикл, представляет собой знаменитую "квадратуру круга", которая по сути есть деление круга на четыре части, символизирующее собой соединение духа и материи. (Источник)
Почему ныне во всем мире используется именно десятеричная система счисления?
Фильм "Степени десятки"4-е треугольное число.Третье тетраэдральное число.Сумма первых четырёх факториалов (0! + 1! + 2! + 3!).Сумма первых трёх простых чисел (2+3+5). Эти числа также представляют последовательность простых чисел между его наименьшим и наибольшим делителем
Пословицы и поговорки Бык, испугавшийся льва, десять лет страдает животом.В деревне десять домов, а старост - двенадцать. Даже на вора десять лет надо учиться.Десяти сторожам не устеречь одного вора. Десять дервишей уснут на одной рогоже, а два царя в одном царстве не уживутся. Десять друзей вроде бы мало, а один враг — много. Десять заповедей пришли к нам с неба, потому их трудно выполнять на земле. Десять знающих не стоят одного, который дело делает.Десять лет я не мог найти дорогу назад, а теперь позабыл, откуда пришел.Десять пальцев сильнее, чем один палец. Десять человек — десять оттенков цвета. Добру и за десять лет не научишься, а для зла и одного дня достаточно. Дорогой пять, а прямо десять.Его десятью пестами в ступе не уловишь. Если красота десять, то девять из десяти — одежда. Если мил друг, и десять вёрст - не крюк.За десять лет даже горы и реки меняются. Избавишься от одного порока - вырастут десять добродетелей. Из десяти монахинь девять — блудницы, а одна не в своем уме. И среди десяти пальцев не бывает одинаковых. Как ни дешева корова, она дороже десяти шиллингов. Кто летом потеряет один день — зимой потеряет десять.Ловкий нагрузил десять телёг, а сильный всего лишь одну.Лучше знать одно ремесло хорошо, чем десять плохо. Лучше десять раз поворотить, чем один на мель сесть. Лучше один весельчак, чем десять зануд.Лучше один мудрый, чем десять глупых.Мастер один, а подносчиков десять.На гору десять тащат, а под гору и само катится. На руках, на ногах по десяти перстов. Один дурак бросит в воду камень - десять умных не достанут.Один испеченный хлеб лучше десяти фунтов теста. Одна птица в руках лучше, чем десять на дереве. Одна своя корова лучше, чем десять соседских.Одно дерево срубишь - десять посади.Одно проникновенное слово сломит душу скорее, чем десять ударов.Одну ветку тронешь — десять закачаются.Пальцев десять, но какой ни укуси - одинаково больно. Пока до начальника доберешься, раз десять споткнешься.После родов женщина десять дней в гробу стоит (т. е. больна). Пошел весной заяц сам-друг в поле, а воротился сам-десят оттоле.Прямику одна дорога, поползню десять.Русский час - десять, а немецкому и конца нет. Сделанное десятью ударами портят одним. Скажешь слово, а прибавят десять.Сорока с тыну, а десять на тын. Трус умирает десять раз; бесстрашный только однажды.Туды-сюды рубль, туды-сюды два, корову торговала, семь рублей давала, вот те и все десять рублей!Ты ему слово, а он тебе десять. Угостишь других десятью кусками мяса, и тебя угостят когда-нибудь куском.У озорного человека десять мучений, а у проказника - двадцать.У парня одна мысль, а у девушки десять. У храбреца десять доблестей: одна - отвага, девять – ловкость.Умный услышит раз, а догадается десять раз.Хороший совет стоит десяти изрядных.Чего не сделаешь один, сделают десятеро.Человек десять раз извернется: раз в слона, а в другой - в комара обернется.Человек доброго нрава десять раз в гостях переночует, а человек со злым языком в степи переночует.Человеческий яд равен десяти змеиным.ещё пословицы...ПесниScorpions - 10 Light Years AwaySkyclad - Ten Little Kingdoms
Аквариум - Десять стрел
Александр Розенбаум - Великан
Алексей Романов - 10 поцелуев
Кристина Орбакайте - 10 Вечеров
Машина времени - В добрый час
Ольга Зарубина - На теплоходе музыка играет
Руки Вверх - 10 лет
СерьГа - Десять Здравствуй
Загадки1. Твои помощники - взгляни - десяток дружных братцев. Как славно жить, когда они работы не боятся (пальцы).2. Ёжик вырос в десять раз, получился … (дикобраз).
3. Проживают в умной книжке хитроумные братишки. 10 их, но братья эти сосчитают все на свете (цифры).
4. Есть у меня работники, во всем помочь охотники. Живут не за стеной - день и ночь со мной: целый десяток, верных ребяток! (пальцы).
5. На десятки верст - разноцветный мост. Только вот по нему не шагать никому (радуга).
mar4586.narod.ru
Для записи чисел люди придумали десять знаков, которые называются цифрами
Разряды и классы
Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
С помощью десяти цифр можно записать любое натуральное число.
От количества знаков (цифр) в числе зависит его название.
Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число - 1, наибольшее - 9.
Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число - 10, наибольшее - 99.
Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число - 100, наибольшее - 999.
Каждая цифра в записи многозначного числа занимает определённое место - позицию.
Разряд - это место (позиция), на котором в записи числа стоит цифра.
Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.
Разряды отсчитываются с конца числа.
Разряд единиц - это самый младший разряд, которым заканчивается любое число.
Цифра 5 - означает 5 единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).
Разряд десятков - это разряд, который стоит перед разрядом единиц.
Цифра 5 - означает 5 десятков, если она стоит на предпоследнем месте (в разряде десятков).
Разряд сотен - это разряд, который стоит перед разрядом десятков. Цифра 5 означает 5 сотен, если она стоит на третьем месте от конца числа (в разряде сотен).
Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра 0 (ноль).
Пример. В числе 807 содержится 8 сотен, 0 десятков и 7 единиц - такая запись называется разрядным составом числа.
807 = 8 сотен 0 десятков 7 единиц
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.
Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.
Классы и разряды
В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.
Класс единиц или первый класс - это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен.
Пример.
| Числа | Класс единиц (первый класс) | ||
| сотни | десятки | единицы | |
| 6 | - | - | 6 |
| 34 | - | 3 | 4 |
| 148 | 1 | 4 | 8 |
Класс тысяч или второй класс - это класс, который образуют следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч.
Пример.
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 5234 | - | - | 5 | 2 | 3 | 4 |
| 12 803 | - | 1 | 2 | 8 | 0 | 3 |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
Напоминаем, что 10 единиц разряда сотен (из класса единиц) образуют одну тысячу (единицу следующего разряда: единицу тысяч в классе тысяч).
10 сотен = 1 тысяча
Класс миллионов или третий класс - это класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов и сотни миллионов.
Единица разряда миллионов - это один миллион или тысяча тысяч (1 000 тысяч). Один миллион можно записать в виде числа 1 000 000.
Десять таких единиц образуют новую разрядную единицу - десять миллионов (10 000 000).
Десять десятков миллионов образуют новую разрядную единицу - сто миллионов или в записи цифрами 100 000 000.
Пример.
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | - | - | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | - | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 0 | 7 | 2 | 0 |
Как прочитать многозначное число
Чтобы прочитать многозначное число, надо назвать по очереди слева направо число единиц каждого класса и добавить название класса.
Не произносят название класса единиц, а также класса все три цифры которого нули.
Например, число 134 590 720 читаем: сто тридцать четыре миллиона пятьсот девяносто тысяч семьсот двадцать.
Число 418 000 547 читаем: четыреста восемнадцать миллионов пятьсот сорок семь.
На нашем сайте для проверки своих результатов вы можете воспользоваться калькулятором разложения числа на разряды онлайн.
Чтобы легче запомнить, как читать и записывать многозначные числа, советуем использовать выше приведённую "Таблицу классов и разрядов".
neosee.ru
Основные типы значков
Основные типы значков
Основные типы значков
"Ударнику Сталинского призыва"
|
Тип (и жаргонное название)
|
Основные части (без элементов крепления к одежде) |
Диапазон номеров |
Количество вариантов |
Comments
|
|
Тип 1 "Тройной" |
Сборный на заклёпках, с номером на реверсе Основные части значка : - накладка (паровоз, серп, молот), - шестиугольная гайка со звездой, - основа знака с флагами. |
77--55063 |
Варианты штемпелей не обнаружены.
|
|
|
Тип 2 "Двойной" |
Сборный, без заклёпок, с номером на реверсе Основные части значка : - накладка (паровоз и гайка), - основа знака с флагами. |
55339--75819 |
Варианты штемпелей не обнаружены. |
|
|
Тип 3 "Плоский с номером" |
Цельноштампованный с номером на реверсе. Реверс плоский, с впадиной на месте паровоза. |
76124--79396 |
Варианты штемпелей не обнаружены. |
|
|
Тип 4 "Плоский без номера" |
Цельноштампованный без номера на реверсе. Реверс плоский, с впадиной на месте паровоза. |
Без номеров |
Четыре варианта штемпелей реверса. |
|
|
Тип 5 "Контррельеф" |
Цельноштампованный без номера на реверсе. Реверс с контррельефом, повторяющим аверс. |
Без номеров |
Почти два десятка вариантов штемпелей и оформлений аверсов значков. |
|
Прочие типы значков
|
Дубликаты |
Значки, выданные взамен утерянных |
Единичные экземпляры |
|
|
Парадоксы |
Комбинированные (ремонтные ?) экземпляры |
Единичные экземпляры |
|
|
Браки |
Значки с технологическими дефектами |
Единичные экземпляры |
|
| Копии |
Специально изготовленные значки, копирующие оригиналы. |
Единичные экземпляры |
|
|
Fakes (подделки) |
Подделки и фантазии |
Уже встречаются! |
|
www.vk-badges.narod.ru
Символы, которых нет на клавиатуре
seo-mayak.com
история популярных компьютерных символов / Offсянка
С тех пор как человек осознал, что может сделать рисунок, он не переставая совершенствовал свои навыки в этом умении. Он рисовал всё, что видел и о чём думал. И это было не просто развлечение или бесполезное действие. Визуальные образы на глине, камне, холсте и прочем помогали дополнить человеческую речь и служили своего рода средством коммуникации. Благодаря этому умению была изобретена письменность — универсальная система символьной коммуникации, которая заметно ускорила дальнейший темп развития человечества.

Практически любая вещь несет на себе следы этого очень важного открытия: на нашей одежде имеются ярлыки с указанием размера и страны-производителя, на бытовой технике полно надписей, касающихся режимов работы и функций устройств, на светильниках обозначена допустимая мощность используемых ламп и так далее. И если очень внимательно присмотреться ко всем этим вещам, можно заметить, что, помимо простого текста, на разных устройствах используются также вспомогательные символьные обозначения.
Их значение очень велико. Стоит взять в руки любое электронное устройство — и вы безошибочно определите, какую именно нужно нажать кнопку, чтобы его включить, увеличить или уменьшить яркость на экране, отключить звук и так далее. Посмотрев на одни только значки на корпусе ноутбука, можно сделать вывод о текущем режиме работы или о начинке мобильного компьютера. Понятные современному человеку обозначения используются так давно, что мы не задумываемся, откуда все они взялись. Давайте сегодня вспомним о том, как родились самые популярные знаки.

Символьные знаки существенно упрощают передачу смысла, они более емкие и воспринимаются быстрее. Например, для водителя лучший способ быстрого предупреждения — яркий знак на дороге. Если бы на щитах писали сообщения вроде: «На данном участке дороге необходимо быть внимательным, поскольку ее могут перебегать дети», водители просто не успевали бы читать все это и реагировать.
⇡#Кнопка включения
Символ, обозначающий кнопку включения электронного устройства, знаком всем, ведь именно с него начинается работа подавляющего большинства электроприборов.

Впервые его прототип можно было увидеть на военной аппаратуре времен Второй мировой. Однако в то время его смысл был неочевидным (по причине, о которой мы расскажем ниже), и повсеместно он стал применяться позднее, с того момента, когда в обиход вошли интегральные микросхемы, которые начали появляться примерно в конце шестидесятых годов прошлого века.

Джек Килби (Jack Kilby) — человек, получивший Нобелевскую премию за открытие интегральной микросхемы
Электрическое состояние и работа логических элементов характеризовались уровнями сигналов на его входах и выходе. Сигнал небольшого (или нулевого) напряжения, уровень которого не превышал некоторого значения (0,3–0,4 В), в соответствии с двоичной системой счисления было принято называть логическим нулём (0), а сигнал более высокого напряжения (по сравнению с логическим нулём) — логической единицей (1). Эти простые символы послужили наглядным обозначением «выключено» и «включено».
В середине семидесятых годов в СССР выпускались цветные телевизоры «Электрон». Размер лампового телевизора, равно как и его вес, по современным меркам были огромными: в одиночку перенести такое устройство было довольно сложно. Переключение между каналами осуществлялось с помощью массивного селектора каналов ПТК, или переключателя телевизионных каналов (в восьмидесятых годах этот элемент канул в Лету, уступив более надежным кнопочным переключателям и невероятно удобным ИК-пультам ДУ). На передней панели, под переключателем каналов, присутствовала «качелька» для включения/выключения телевизора. Эта деталь удивительным образом схожа с аналогичным элементом на современных плеерах и всяческой бытовой технике. На самом деле «качелька» была лишь декоративной насадкой, которая с помощью несложного рычага осуществляла движение спрятанного тумблера. В модели «Электрон-710» по краям «качельки» на панель телевизора нанесены словесные обозначения «вкл.» и «выкл.».

Но если взять последующие модели этого же завода, «Электрон-711» или «Электрон-714», которые практически не отличались по дизайну от предшественника, можно заметить, что режимы включения обозначены как «0» и «I». Объединив эти два символа, мы получим знакомый всем логотип кнопки включения.

Официально стандарт обозначения кнопки включения устройства был утвержден в 1973 году Международной электротехнической комиссией (International Electrotechnical Commission). Знаку в виде вертикальной линии на фоне разорванного круга было дано несколько расплывчатое определение: «состояние ожидания включения» (standby power state). Чуть позже другая организация, занимающаяся стандартизацией, Институт инженеров по электротехнике и электронике (IEEE), упростила это определение, сократив его до простого «питание» (Power).
Для современного человека ноль и единица — это самые базовые средства счета. Однако если задуматься, то понятие «ноль» не столь очевидно, как другие цифры. Человек учится считать не с нуля, а с единицы. В силу ограниченного воображения и прагматичности мышления ему трудно соотнести что-то с «ничем». Поэтому, например, древние греки или римляне в своей системе счета не знали цифры ноль. Египтяне, шумеры и китайцы неосознанно использовали ноль, но не как цифру, а как пустоту, место для заполнения внутри числа. Ноль, равно как и прочие цифры, не совсем корректно называемые сегодня арабскими, берут свое начало в Индии, где была создана десятичная система счисления с цифрами, которые после незначительных изменений обрели знакомый сегодня вид. Если сравнить написание цифр древними индийцами и арабскую систему цифр, можно увидеть, что, например, 2 и 5 в современном написании гораздо больше похожи на индийские символы.
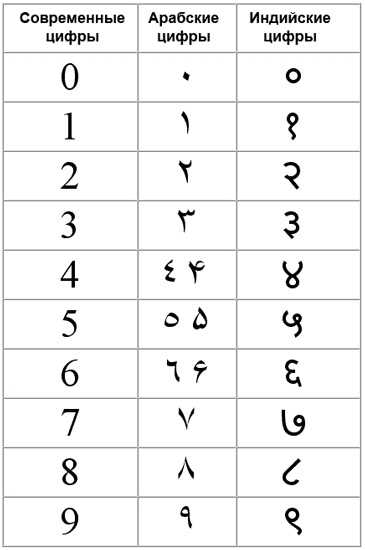
Первое свидетельство возникновения цифры ноль можно увидеть на стене храма в центральной Индии, в крепости Гвалиор. Там можно найти надписи на санскрите, датируемые примерно девятым веком (хотя, вероятно, ноль использовался древнеиндийскими математиками еще раньше). Они содержат новый знак в виде круга. По одной из версий, округлая форма знака «ноль» родилась в результате экспериментов древних математиков. Многие из них предпочитали делать вычисления с помощью каких-то предметов. Так, например, в Китае для счета использовали счетные палочки. В Индии для решения задач использовались камни. Разложив их на земле, математики перекладывали их с места на место, а под убранным камнем оставалась округлая ямка — то самое «ничего», или ноль. Любопытно, что открытие цифры ноль примерно совпадает с появлением философского понятия «ничто», шуньята, концепции небытия и вечности, характерной для древнеиндийской культуры. То ли культурный аспект стимулировал научные изыскания у людей того времени, то ли наоборот — математические выкладки заставили их углубиться в философские размышления. Одно небольшое открытие, а какой поворот в истории человечества — от нового удобного способа счета до символа кнопки включения любого прибора!
⇡#Режим ожидания
С появлением все более сложных устройств человек столкнулся с необходимостью применения режима ожидания, суть которого состоит в том, что устройство готово к работе, но не выполняет свои функции. Режим обеспечивал быстрый запуск и экономил время на настройку некоторых опций устройств. Например, до появления данной функции телевизор включался довольно долго, «прогреваясь» с десяток секунд, в то время как в режиме ожидания он потреблял минимальное количество энергии и мгновенно был готов к работе.
Новшество удобное, но вот донести до неискушенного потребителя, что означает «режим ожидания», было не очень просто. Поломав голову, дизайнеры предложили очень удачное сравнение — человеческий сон. Во время ночного отдыха функциональность живого организма замедляется, но при этом возможно быстрое пробуждение и активная деятельность. Так родился значок в виде полумесяца, а режим ожидания превратился в «режим сна», или в «спящий режим».

⇡#Кто придумал курсор?
Изображение курсора появилось на экране вместе с изобретением первого компьютерного манипулятора — мыши. Свою работу над мышкой Дуглас Энгельбарт (Douglas Engelbart) начал еще в 1961 году. Работать ему было очень сложно, поскольку манипулятор создавался для устройств узкой специализации.

В то время компьютеров как таковых, можно сказать, не было, и представление о том, как они будут выглядеть, только-только начинало формироваться. И, понятное дело, возникла необходимость в точном позиционировании объектов на экране.
Изобретатель первой компьютерной мышки может служить примером для тех, кто не чувствует уверенности в своих силах. В глазах сегодняшних пользователей Энгельбарт выглядит гением, ведь его открытие пережило самого автора, став основным человеко-машинным интерфейсом на ближайшие десятилетия. Безусловно, Дуглас был очень изобретательным и проницательным, однако свои таланты этот человек развивал, собирая и тщательно анализируя труды других. И кстати, он не был наделен сверхспособностями в схемотехнике. Несмотря на то, что отец Энгельбарта держал магазин по продаже и ремонту радиоприемников, изобретатель мыши признался в одном интервью, что сам попытался сделать лишь несколько детекторных приемников, но ни один из них так и не заработал.
Неизвестно, была бы придумана компьютерная мышь, если бы Дуглас не прочел труд американского инженера Вэнивара Буша (Vannevar Bush).

В 1945 году в журнале The Atlantic вышло его эссе «Как мы можем мыслить», где Вэнивар рассуждает о необходимости хранения информации большого объема с удобной системой навигации. Проводя параллель с человеческим мышлением, Буш точно описывает гипертекстовую систему (некое гипотетическое устройство под названием «Мемекс») с возможностью использования ассоциативных ссылок и примечаний. Энгельбарту и его коллегам удалось воплотить в реальность многие из идей Вэнивара.

Изобретение мыши было лишь маленькой частью амбициозного проекта по расширению человеческого интеллекта, который в оригинале носил название Augmenting human intellect. За этим громким названием стоит детальная разработка структуры компьютера и формирование принципов общения пользователя с устройством. Энгельбарт собрал команду ученых и единомышленников, которая составила отдел Augmentation Research Centre при Стэнфордском исследовательском институте.

В сохранившемся до наших дней техническом описании проекта можно увидеть множество точных и поразительных предсказаний относительно компьютерной техники. В рамках этого проекта Энгельбарт утверждал, что компьютер должен состоять из клавиатуры, ЭЛТ-экрана, мыши, также он рассказывает о базовых принципах работы с файлами и папками. Кроме того, Дуглас подробно описывал, почему удобно использовать новый компьютерный манипулятор для редактирования текста и чем он лучше уже существовавших в то время разработок — «светового пера» и «джойстика». Изобретатель компьютерной мыши впервые познакомил всех с такой фантастически полезной вещью, как буфер обмена, и раскрыл смысл команд «скопировать», «вырезать», «вставить». Дуглас объяснил, как все это работает, настаивая на концепции «интерактивного редактирования», или NLS («oN-Line System»).
В книгах и прессе часто говорят, что Дуглас сам назвал свое устройство мышью, но это не так. Для технической документации устройство называлось очень скучно — XY Position Indicator for a Display System. Во время работы над ним кто-то в лаборатории заметил, что манипулятор с хвостом-проводом похож на живого грызуна, и название прижилось. Однако, как утверждал сам Энгельбарт, кто именно из его коллег первым догадался назвать компьютерную мышку мышкой, никто и не помнит.
Долгое время команда Дугласа Энгельбарта экспериментировала с дизайном манипулятора. Даже когда инженеры «нащупали» верное направление концепции и формы, они все равно продолжали искать способ сделать новое устройство лучше и удобнее. Для этого, например, они развернули провод, так, чтобы он шел от пользователя к компьютеру. В первых версиях компьютерного манипулятора он выводился в сторону пользователя, что приводило к тому, что провод путался под рукой и мешал. Первая компьютерная мышь была громоздкой, в деревянном корпусе с двумя перпендикулярно вращающимися колесами, которые передавали на датчики информацию о движении указателя по вертикали и горизонтали. Сперва кнопка была одна, но Дуглас хотел сделать более функциональный манипулятор, в идеале — с пятью кнопками, под каждый палец руки.

Однако с этой идеей ничего не получилось, и пришлось оставить максимальное количество кнопок, с которыми было удобно работать, — три. Нехватку клавиш на мыши предлагалось компенсировать дополнительным пятикнопочным клавиатурным блоком. Последний действительно позволял ускорить ввод данных — при использовании комбинаций кнопок, на нем можно было набирать текст — как с большой клавиатуры. Но на практике этот модуль оказался сложным в освоении, так как пользователю нужно было запомнить большое число сочетаний клавиш.
Некоторое время Энгельбарт искал спонсоров своих разработок и даже вел переговоры с NASA, однако крупнейшее космическое агентство не заинтересовалось его изобретением из-за того, что мышь не работала должным образом в условиях невесомости.
⇡#Курсор за семью печатями
Стоит отметить, что проект Дугласа Энгельбарта вообще-то был не первым компьютерным манипулятором. Нечто подобное уже имелось в распоряжении военных разных стран, и эти разработки также могли бы сделать переворот в компьютерной индустрии, если бы их не держали под грифом «Секретно». И конечно, форма курсора, могла бы быть иной — например точкой, треугольником или еще чем-нибудь.
Так, например, в далеком 1946 году совсем молодой инженер Ральф Бенджамин (Ralph Benjamin) сконструировал для британского флота первый трекбол roller ball, выполняющий функции указателя точки на радаре. Во время войны Ральф потерял родителей в ходе геноцида евреев, а сам был вынужден бежать из Германии в Швейцарию, а позже и в Англию.

В возрасте 91 года профессор Ральф Бенджамин с огромным удовольствием рассказывает журналистам, что изобрел курсор за двадцать лет до Энгельбарта.
Чуть позднее, в 1952 году, в условиях строжайшей секретности, похожий манипулятор сделали Том Крэнстон (Tom Cranston), Фред Лонгстаф (Fred Longstaff) и Кенион Тэйлор (Kenyon Taylor). Забавная деталь — в качестве «шарика» в конструкции этого трекбола инженеры использовали шар для канадского пятипинового боулинга. Это устройство был частью системы DATAR, которая расшифровывалась как Digital Automated Tracking and Resolving («цифровое автоматическое слежение и расчет»).

По замыслу военных, она должна была собирать информацию с сенсоров на разных кораблях и выводить их на экран. Оператор мог просматривать данные о кораблях с места боевых действий, выбирая их манипулятором. Но когда трекбол был сделан, стало понятно, что это устройство слишком опережает свое время, а доработка и без того дорогой системы DATAR (бюджет составил почти два миллиона канадских долларов) требует еще большего финансирования.
Пока на другой стороне планеты думали, что им делать с этим трекболом, в СССР с 1953 по 1957 год сконструировали и запустили в работу первую протомышь, которая, само собой, тоже использовалась военными структурами.
На вооружение отечественных систем ПВО была принята система «Воздух-1», разработанная под началом конструктора Михаила Ивановича Михайлова.

Согласно информации из специальной учебной литературы, она была предназначена для полуавтоматического съема, автоматической передачи, обобщения и отображения данных о воздушной обстановке на индикаторных устройствах системы, приборного наведения истребителей-перехватчиков на воздушные цели противника, управления войсками ПВО и взаимодействия с ними. Говоря проще, эта система позволяла сопровождать до 40 целей (в том числе и своих перехватчиков) и наводить перехватчики на несколько целей одновременно. Частью «Воздух-1» являлся комплект аппаратуры АСПД-I, содержащий первичный индикатор ввода и передачи высоты и цифр (ИПН или ИПН-1) — советский вариант компьютерного манипулятора.

На этом снимке показан макет аппаратуры автоматизированной системы управления радиолокационного поста ВП-02у. Обратите внимание на зеркальный «коврик» и манипулятор в правой части стенда. Чем не двухкнопочная мышь?

Да и функции этот инструмент выполняет практически те же самые. И все это — задолго до официальной демонстрации изобретения Дугласа Энгельбарта.
Наземная система автоматического наведения на цель самолетов-перехватчиков в США (Semi-Automatic Ground Environment), созданная приблизительно в это же время, также имела манипулятор-пистолет, которым можно было водить непосредственно по радару. Сердцем этой системы был компьютер AN/FSQ-7, созданный компанией IBM.

⇡#Почему курсор наклонен?
Но вернемся все-таки к курсору. Первыми его могли увидеть участники Осенней объединенной компьютерной конференции (Fall Joint Computer Conference) 9 декабря 1968 года. Первый курсор в виде стрелочки указывал положение на экране, где выполнялось редактирование текста.

Первый курсор (под словом MOVE)
Демонстрация возможностей компьютерного манипулятора Дугласа Энгельбарта была записана на видео и вошла в историю как «Мать всех презентаций» (The Mother of all Demos).
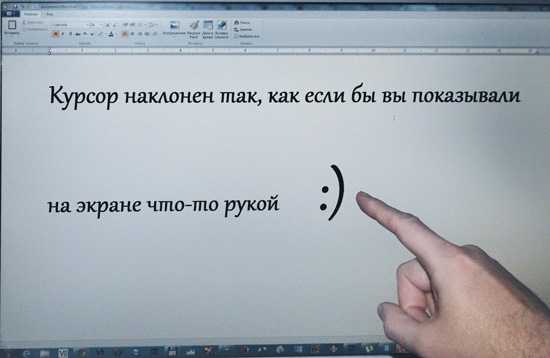
Но если вы внимательно всмотритесь в изображение первого курсора, то заметите, что он несколько отличается от современного указателя на экране монитора. Он прямой, в отличие от привычного нам курсора, который имеет наклон в левую сторону. Зачем же его наклонили?
Спустя некоторое время после изобретения мыши команда Augmentation Research Centre стала распадаться, часть ученых перешла в Xerox PARC, где продолжила совершенствовать манипулятор. Вскоре компания Xerox смогла похвастаться первыми ПК, которые управлялись не только командами с клавиатуры, но и с помощью первых моделей компьютерных мышей.

Разрешение экрана в первых моделях компьютеров Xerox Alto составляло 808 точек по вертикали и 606 точек по горизонтали. Из-за этого ограничения было невозможно добиться четкого отображения вертикального курсора, поэтому его пришлось «повернуть». Новый курсор был лучше и по ряду других причин. Вертикальный курсор мог сливаться с символами на экране, а наклоненный — нет. Элементы интерфейса операционной системы Star содержали главным образом вертикальные и горизонтальные линии, на фоне которых визуально определить положение наклоненного курсора было проще.

Также не стоит забывать о том, какая низкая производительность была у компьютеров в то время. При создании курсора разработчикам казалось вполне логичным разместить «горячую точку» на острие курсора с координатами (0;0) — это позволяло сэкономить несколько циклов просчета подпрограммой, определяющей положение курсора.
Что же касается вопроса «Почему курсор наклонен именно в левую сторону?», то и тут найти ответ несложно. Попробуйте указать пальцем на экране монитора на какую-нибудь деталь. Видите, он наклонен в ту же сторону (если только вы не левша). Поэтому и курсор с наклоном влево выглядит нагляднее.
⇡#История значка @ — где «собака» зарыта
У знака @ есть множество имен. Есть официальное имя — «коммерческое at». А есть еще масса прозвищ, которые пользователи активно выдумывают на ходу. Какие только клички не присваивались этому знаку — «ухо», «загогулина», «хобот», «бублик», «плюшка», «обезьяна», «баран» и еще десятки других. Ну а самое популярное имя (по крайней мере, в России) — «собака».

Любопытно, что ассоциация с разными животными у пользователей различается, в зависимости от места проживания. Например, на Тайване этот знак зовут «мышкой» (как они только не путаются при этом с компьютерной мышью?), в Венгрии это — «червяк» и «клещ», в Греции — «уточка», в Италии — «улитка». В Финляндии этот знак называют «кошачий хвостик» или «мяу-мяу». Проголодавшиеся пользователи из Чехии и Словакии видят в нашей «собаке» вполне съедобный рулетик из сельди — «рольмопс», а в Израиле его и вовсе называют «штрудель».
Но почему же у нас прижилась «собака»? Видимо, есть причины, по которым именно это животное ассоциируется у наших пользователей с @. Возможно, все началось с восьмидесятых годов, когда в СССР была произведена линейка ЭВМ под названием ДВК («диалоговый вычислительный комплекс»). Специфическое отображение этого знака на дисплее делало @ (при наличии воображения) похожим на собачку. И этот символ отображался на экране при каждом включении ДВК.
Имеется также версия, что произношение английского at созвучно с лаем собаки. А еще, по словам геймеров с большим стажем, в девяностых годах существовала компьютерная игра Adventure с текстовой графикой, где у главного героя был помощник — собака. На экране она была показана знаком @. Несмотря на наши тщательные поиски, найти этот раритет нам так и не удалось.
Какая из вышеперечисленных версий правильная — вряд ли кто-нибудь сможет сказать точно. Выбирайте любую.
Особый смысл знаку @ придал программист Рэймонд Сэмюэль Томлинсон (Raymond Samuel Tomlinson), который работал в компании BBN (Bolt, Beranek and Newman) и принимал участие в работе над проектом ARPANET — прообразом современной сети Интернет.

Компьютерная сеть ARPANET (Advanced Research Projects Agency Network) была создана в 1969 году с подачи Министерства обороны США как альтернативный и надежный способ передачи данных на расстояние. Спустя два года Томлинсон предложил оригинальный способ отправки электронной почты на разные компьютеры сети ARPANET — разделяя пользователя и имя его компьютера с помощью @.

На клавиатуре было много символов, и теоретически можно было бы взять любой, но тут повлияла игра слов. Дело в том, что символ @ появился задолго до компьютеров и даже присутствовал на печатных машинках в виде отдельной клавиши. Напечатать «собаку» можно было еще в конце XIX века на машинках Underwood.

Знак @ использовался в коммерческой и деловой переписке, обозначая предлог «по», «при» или «на». Так, скажем, если необходимо было написать «цена на товар составит 100 долларов за штуку», достаточно было напечатать @$100. Таким образом, разделив почтовый адрес предлогом at, Рэймонд Томлинсон получил буквальное определение адреса — «такой-то пользователь на (@) таком-то компьютере». По иронии судьбы первое же письмо, посланное с символом @, оказалось спамом — оно содержало бессмысленный набор символов, с помощью которого Рэй проверил работу электронной почты.
Интересно, что программист не сразу осознал значение своего открытия. Более того, демонстрируя отправку и получение электронной почты в сети своему сослуживцу Джерри Барчфилу (Jerry Burchfiel), Томлинсон предупредил: «Знаешь, не говори про это никому. Вообще-то это не то, чем мы должны тут заниматься».
⇡#USB: дьявольский логотип
Изображение, символизирующее USB-подключение, можно найти на любом кабеле или рядом с гнездом для подключения. Созданное в рамках спецификации USB 1.0 обозначение USB-порта представлено в виде тройной линии, напоминающей фрагмент печатной схемы. В вертикальном положении этот знак приобретает вид трезубца, что неслучайно.
Данный символ дизайнеры позаимствовали из образа бога водной стихии Нептуна (Посейдона) в древней мифологии. В древнегреческой мифологии могучие вилы Посейдона имеют особое значение — это и грозное оружие, с помощью которого бог разрушает скалы, и символ власти. Как и на трезубце Посейдона, центральное острие выступает чуть больше, но если в греческой мифологии это означает жезл Зевса и признание силы старшего брата (два остальных «зуба» на трезубце Посейдона — это рогатина второго брата, Аида, бога подземного царства мертвых), то в случае с логотипом USB выступающий элемент не имеет смысловой нагрузки. Вместо шипов на трезубце USB-логотипа нарисованы три основные геометрические фигуры — круг, квадрат и треугольник. Эти простейшие фигуры символизируют разнообразие периферийных устройств, которые могут быть подключены к единому интерфейсу USB.
Забавно, что трезубец с USB-логотипа послужил предметом спора среди некоторых верующих. Четыре года назад он вызвал не совсем адекватную реакцию у отдельных религиозных служителей Бразилии, которые окрестили его инструментом дьявола и призвали пользователей отказаться от благ данной технологии, используя вместо нее Firewire или Bluetooth. Если следовать этой странной бразильской логике, то вслед за USB нужно было бы запретить всю продукцию Apple с логотипом в виде надкушенного яблока, а заодно и выбросить десертные вилки для торта с тремя зубьями. Как говорится, от греха подальше.

⇡#Bluetooth: знак короля Синезуба
Мобильное устройство невозможно представить без поддержки беспроводных сетей. Без возможности загружать данные с других устройств и передавать их портативный гаджет попросту бесполезен. На данный момент существует две наиболее популярные технологии передачи данных в локальных сетях без проводов — Wi-Fi и Bluetooth. У каждой из них есть свой логотип.
Взгляните на синий значок рядом с голубой лампочкой на вашем ноутбуке. Не замечаете ничего странного? Сравните его с другими символами на компьютере. Каждый рисунок более или менее понятен, так как его можно «расшифровать». Например, аккумулятор нарисован в виде батарейки, а управление громкостью помечено на клавишах изображением динамического излучателя. Но как бы вы ни фантазировали насчет логотипа Bluetooth, вряд ли догадаетесь, что за «кракозябра» на ней изображена.

Чтобы понять, откуда взялся логотип, нужно вспомнить о том, как и где появилась эта технология.
А родилась она на родине викингов, в Швеции, под началом известной фирмы Ericsson. Данную технологию разработали в 1994 году два инженера — швед Свен Маттиссон (Sven Mattisson) и голландец Яаап Хаартсен (Jaap Haartsen). Причем Маттиссон не только создал Bluetooth, но и косвенно повлиял на то, что эта технология была названа в честь короля Харальда Синезуба, одной из самых значительных фигур в истории Скандинавии.
Свен Маттиссон
Название Bluetooth предложил Джим Кардаш (Jim Kardach), который участвовал в организации переговоров между Intel (где и работал Кардаш), Ericsson, IBM, Toshiba и Nokia относительно разработки единого стандарта беспроводного соединения. В конечном итоге эти переговоры закончились появлением Special Interest Group (SIG), утвердившей стандарт Bluetooth.

Как-то раз Джим поинтересовался у Свена, что за книгу он сейчас читает. Тот ответил, что это — исторический роман шведского писателя Франца Гуннара Бенгтссона (Frans Gunnar Bengtsson) о викингах. Кардаш заинтересовался этим автором и в скором времени тоже увлекся историей древней Скандинавии. Прочитанная литература очень увлекла Джима, в особенности он был впечатлен личностью древнескандинавского короля Харальда Синезуба. За время своего правления Харальд сделал немало полезных дел — объединил разрозненные земли, а также ввел христианство на территории Норвегии и Дании.
Кардаш предложил имя короля в качестве рабочего названия проекта, аргументированно обосновав свой выбор. Название Bluetooth оказалось очень метким и точным. Король Синезуб объединил скандинавские племена, а новая технология объединяла разрозненные разработки в области беспроводной передачи данных с малой мощностью. Bluetooth поставил точку в многообразии стандартов, существовавших в то время.
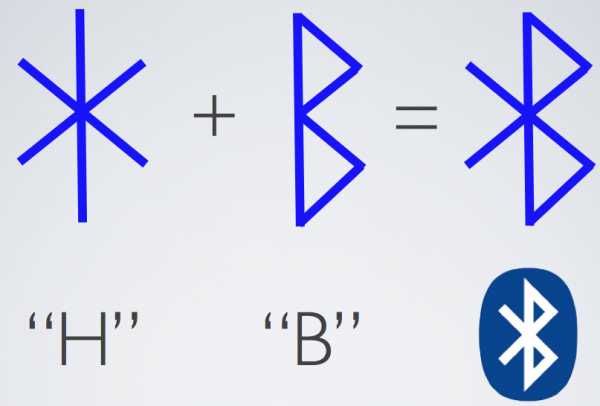
Знак, который стал логотипом технологии Bluetooth, образован двумя древнескандинавскими рунами. Первая называется «хагалаз» (Hagall), другая — «беркана» (Berkanan). Эти две руны повторяют буквы латинского алфавита H и B. Вместе же они составляют инициалы короля Харальда Синезуба. По этой же причине логотип Bluetooth имеет синий цвет.
Существует много версий появления у короля такого прозвища, например из-за дорогих одеяний редкого синего цвета, которые подчеркивали его высокий статус. Строго говоря, слово «синий» — не совсем верный перевод с древнескандинавского языка, по смысловому значению оно ближе к «темный». Возможно, король имел проблемы с зубами, отчего они и потемнели. Есть также версия, что Харальд просто очень любил чернику.

Название Bluetooth запоминалось сразу, оно очень понравилось журналистам, которые стали обыгрывать его в своих новостных заголовках, поэтому рабочее название решено было оставить. Хотя справедливости ради нужно сказать, что других вариантов имени почти и не было. Было лишь одно достойное альтернативное название этой технологии — Flirt, которое подкреплялось слоганом «Близко, но без контакта».
⇡#Иконка-гамбургер: самая популярная кнопка
Интерфейс разных компьютерных приложений имеет общие детали. Программы могут отличаться по функциональности, способом установки и запуска, но базовый принцип взаимодействия с пользователем остается неизменным. Мы смотрим на привычное главное меню, изучаем иконки — и мгновенно догадываемся, где и в каком месте интерфейса следует искать ту или иную опцию приложения. Одна из иконок, которая помогает пользователю быстро сориентироваться при знакомстве с новым приложением, называется «гамбургер». На ней нарисованы три горизонтальные черты, одна над другой.
Вероятно, человек, который так окрестил эту иконку, был голоден, и такое расположение линий напоминало слои в бутерброде. А вообще у этой иконки большая история. Она настоящий долгожитель, ей более тридцати лет, и появилась она на самых первых компьютерах.
В нашей публикации «Маленькие истории большого дизайна: от электробритв до планшетов» мы уже затрагивали тему появления первого графического интерфейса, который можно было наблюдать почти полвека назад на компьютере Xerox Alto. В той статье мы даже показывали скриншоты некоторых первых приложений для него. Предок современных ПК был спроектирован командой исследовательского центра Xerox PARC.

Эта разработка оказала колоссальное влияние на последующее развитие компьютерной техники. История сохранила имя Энгельберта, который придумал мышь, Алана Кея, придумавшего концепт ПК, но другие члены группы Xerox PARC, причастные к рождению первого GUI, незаслуженно остались в тени. А ведь без них мы, возможно, не имели бы компьютер в таком виде, в каком он существует сегодня.
Один из талантливых разработчиков семидесятых годов Норм Кокс (Norm Cox), был приглашен в компанию Xerox еще в 1972 году. В первое время, по словам Норма, он был вынужден возиться с «различными винтиками, болтиками и прочими бесполезными пластмассовыми деталями для линейки электропишущих машинок Xerox».
Занятие было не очень интересное, и Кокс развлекал себя тем, что в свободное от время рисовал карикатуры на своих коллег по работе. Сам дизайнер упоминает в своих воспоминаниях, что это увлечение в значительной степени поспособствовало тому, что он смог серьезно продвинуться в карьере. А случилось это после того, как судьба свела его с менеджером по промышленному дизайну Робином Кинкедом (Robin Kinkead), который искал дизайнера для разработки шрифтов печатных машин.
Норм с радостью принял приглашение и сбежал из «прокуренной кутузки» на новое место работы, где ему полагался личный кабинет. Там его талант начал потихоньку раскрываться, появилась возможность творить и экспериментировать. На этой должности он проработал до конца семидесятых. Поскольку отдел, в котором работал Норм, был сервисной организацией, услугами дизайнеров часто пользовались прочие специалисты Xerox, занятые производством тех или иных вещей. Иногда к ним в офис приезжали «странные длинноволосые хиппи из Калифорнии», заводили с сотрудниками не совсем понятные для художника разговоры про компьютеры, брали консультации по вопросам дизайна будущих ПК. В конце семидесятых, под предлогом тестирования, Кинкед раздобыл несколько компьютеров Xerox Alto, один из которых оказался в распоряжении Норма. Заданием Норма и его коллег было проверить, насколько удобен в обращении этот компьютер, какие у него проявляются недостатки, «дружелюбен» ли он по отношению к пользователю и так далее. С этих пор свои карикатуры Кокс уже делал не вручную, а используя простенький графический редактор.

Карикатура на Робина Кинкеда, сделанная на компьютере Xerox Alto
Как-то раз Кинкед сообщил, что подумывает о том, чтобы направить Норма в команду инженеров, работающих над совершенствованием компьютера Xerox Alto и созданием новой оболочки для ПК. Робин долго рассказывал Коксу о новом подходе к общению пользователя с компьютером — с помощью графического интерфейса. «В системе Xerox Star, — говорил Кинкед, — все действия компьютера, все его команды, программы и операции должны визуализироваться с помощью графических иллюстраций. Ты постоянно рисуешь, и у тебя есть талант. Ты определенно можешь помочь им в этом вопросе. Нарисуй на пробу небольшую картинку, проиллюстрируй, например, поступление электронной почты».
Из этой беседы Норм, кажется, мало что понял, хотя и видел прототип такого графического интерфейса на своем ПК. Тем не менее дизайнер постарался оправдать ожидания. Вот первая его первая попытка создать визуальную интерпретацию поступления нового почтового сообщения, сделанная в фирменном карикатурном стиле Кокса. Можно считать, что это одна из первых иконок, хотя, конечно, на классические иконки это непохоже. Команда разработчиков Star нашла эту картинку «интересной».

И хотя изображение было совсем не тем, что было нужно, Норм был приглашен для консультаций и дизайна новой операционной системы Star.
Проектирование компьютеров в семидесятые для большинства людей было чем-то из области фантастики. Норму тоже это представлялось чем-то особенным — занятием, в которое вовлечены серьезные люди. Поэтому перед тем, как выйти на работу на новом месте, молодой дизайнер приготовился как следует — купил костюм-тройку, портфель, начистил туфли. Но когда он оказался в команде, увиденное его потрясло: парни с длинными волосами, собранными в хвостик сзади, шорты, нерасчесанные бороды, пестрые майки и никакого намека на сухих ученых в очках с толстой оправой. «Я выглядел там как пингвин в компании попугаев, — вспоминал потом Норм, посмеиваясь, — но по иронии судьбы эти попугаи стали моими хорошими друзьями, с которыми я проработал много лет».
Операционная система, сделанная в Xerox, впервые использовала парадигму WIMP (window, icon, menu, pointing device — «окно, значок, меню, манипулятор»). В конечном итоге Кокс был назначен ответственным за внешний вид основных элементов новой ОС — он разрабатывал дизайн курсоров, иконок и прочих деталей. Рисовать эти элементы было очень интересной задачей. Норм старался сделать иконки простыми, но «с изюминкой» — дизайнер придавал своим творениям особый выразительный вид, стараясь, чтобы основной экран «просвечивался» через эти пиктограммы. По причине того, что вся работа делалась на квадрате с дюжиной точек по вертикали и горизонтали, художник не мог добиться высокой реалистичности рисуемого изображения. Зато он мог делать края нарисованных объектов неровными, подчеркивая их выразительность. Некоторые из таких иконок практически в неизменном виде дошли до наших дней: пиктограмма папки, документа, калькулятора, мусорного ведра и так далее.
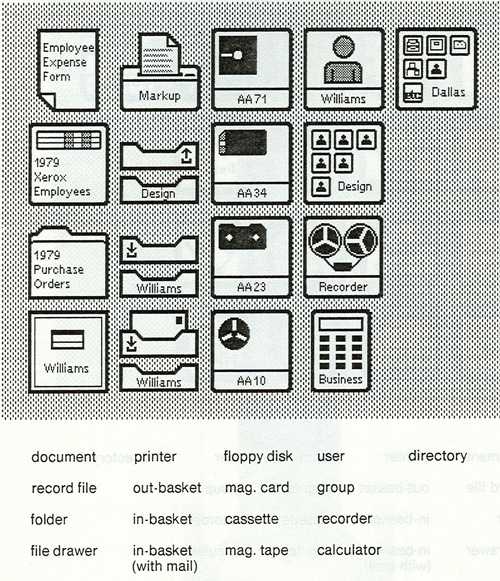
Каждый раз, рисуя новый значок, Норм отталкивался от его функциональности. Например, если элемент называется «папка», то вполне очевидно, что и рисунок должен содержать эскиз папки. Однако иногда приходилось долго искать идею рисунка. Один из элементов был описан в техническом задании Кокса как «контейнер для меню со списком команд». Кокс долго думал, что бы такое изобразить на иконке такого предназначения и под конец нарисовал три горизонтальные черты — ту самую иконку-гамбургер. «Слои бутерброда» в этой иконке, по мнению дизайнера, должны были ассоциироваться у пользователя с каким-то списком, что, в свою очередь, должно было подсказать назначение элемента. Меню, которое открывала иконка-гамбургер, стало прообразом контекстного меню в современных приложениях.
⇡#Клавиша Shift: за сто лет до компьютеров
Все компьютерные клавиатуры объединяет схожий набор клавиш или, проще говоря, раскладка. Пересаживаясь с одного рабочего места на другое, пользователь без проблем начинает работать и не испытывает серьезного дискомфорта от смены клавиатуры. И на любой из них вы найдете клавишу-модификатор Shift. Она значительно расширяет возможности ввода команд с клавиатуры, ведь в сочетании с нажатой клавишей Shift можно набирать знаки препинания, менять регистр букв, а также вводить различные символы.
Удивительно, но эта очень важная клавиша впервые появилась еще в 1875 году. Она была задействована на одной из первых печатных машинок, выпускаемых компанией Remington. Между прочим, Марк Твен тоже купил себе печатную машинку Remington и стал первым автором, представившим машинописную рукопись книги.

Первая модель пишущей машинки, в которой появились клавиши Shift, — Remington 2. В самом первом «реммингтоне» клавиш Shift не было, вместо них имелись две другие: Upper Case и Lower Case.

Они работали так: клавишам назначались два варианта начертания, скажем, большие буквы и маленькие. Печатная машинка могла работать в режиме заглавных символов или в режиме нижнего регистра. Установка этих режимов выбиралась с помощью специального переключателя-рычага, который сдвигал цилиндр с бумагой, помещая его под удар нужного ряда печатающих головок. При нажатии клавиш Upper Case или Lower Case производился временный сдвиг цилиндра и менялся регистр букв. Например, если печатающая машинка работала с маленькими буквами, переключать ее рычагом в режим набора больших букв не всегда было удобно. Гораздо проще было при наборе одновременно с символом нажать Upper Case, и цилиндр временно передвигался для набора больших букв. Отпускание клавиши возвращало исходный режим работы печати.
Начиная со второй редакции печатной машинки, Remington 2, названия этих клавиш заменили более понятным — Shift, что в переводе с английского и означает «сдвиг».

⇡#Контроль над музыкой
Даже дошкольник сообразит, какую кнопку на плеере нужно нажать, чтобы запустился фильм или начала играть песня. Символы на всех устройствах воспроизведения одни и те же — треугольник для запуска, две вертикальные линии — пауза и так далее. Большинство подобных символов родилось в шестидесятых годах прошлого столетия, в эру катушечных магнитофонов.
Как любые другие обозначения на электронной аппаратуре, рисунки над кнопками имеют вполне логическое объяснение. Например, кнопка Play обычно показывается в виде треугольника. На бобинных и кассетных магнитофонах подобный треугольник был нанесен на механическую кнопку таким образом, чтобы указывать острием направление движения магнитной пленки. То же самое касалось и обозначения функции «перемотка», для которой использовался двойной треугольник, также показывающий в сторону перемещения пленки.

Кнопка «пауза» обозначена на большинстве современных проигрывателей в виде двух вертикальных черт. К сожалению, точной информации о том, что подразумевает такой рисунок нет, однако есть несколько очевидных предположений о его появлении. Наиболее вероятным нам представляется ассоциация с термином «цезура».

Мало кто знает, что это такое, хотя сталкивались с этим понятием все. Когда человек декламирует стихи, он читает их с особенным ритмом, делая в нужных местах паузы. Эти паузы определяют ритм и разделяют стихотворение на части. Для вспомогательного обозначения цезуры в тексте используют две вертикальные линии — один в один знак «пауза».
Другая версия знака временного приостановления воспроизведения касается непосредственно музыки, где знак цезуры используется для обозначения в нотной грамоте короткого отрезка тишины неопределенной продолжительности. Для оркестра эту продолжительность устанавливает дирижер. В нотной записи цезура выглядит как две параллельные, слегка наклоненные линии. Не совсем то же самое, что знак «пауза», но очень похоже.
Очень убедительна и теория о том, что символ паузы показывает два вращающихся прижимных ролика, которые удерживают пленку с записанным материалом над головкой чтения или записи.
Красный круг в кнопке записи, по замыслу дизайнеров, должен был напоминать пользователям свет красной лампы, которая загоралась в профессиональных студиях в процессе записи аудио- и видеоматериала. Такая лампа предупреждала всех присутствующих, что шуметь нельзя.

Кнопку записи и иногда — кнопку остановки воспроизведения полностью окрашивали в красный цвет, делая таким же цветом условные обозначения над ними. Эту моду ввел Дитер Рамс, главный дизайнер немецкого бренда Braun, о котором мы рассказывали в статье «Маленькие истории большого дизайна: от электробритв до планшетов».
⇡#Заключение
Рисунки над функциональными кнопками устройств обманчиво просты. Да, все гениальное просто, но не все простое — гениально. Мало просто нарисовать знак, нужно еще и выбрать образ таким, чтобы у пользователя не оставалось никаких сомнений в назначении этой кнопки или переключателя. Иногда у дизайнеров аппаратуры это получается, а иногда — нет. Порой смотришь на какую-то кнопку и недоумеваешь: «Что же все-таки хотел сказать художник этим иероглифом?» Впрочем, теперь вам известны секреты даже самых заковыристых компьютерных логотипов.
Если вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.
3dnews.ru
Штрихи, штришки и штришочки / Хабрахабр
Практика показывает, что если тире или кавычки — это первое, что изучают при появлении интереса к «типографике» (а на самом деле — к грамотному набору текста), то правильное употребление апостро́фа, знаков минут и секунд, знака ударения вызывает почему-то бо́льшие затруднения. На самом деле, всё очень просто, и статья будет довольно короткой. Всё, о чём будет сказано ниже, относится к современной русской традиции типографики.На стандартной PC-клавиатуре есть три символа со штрихами: «'» и «"» на кнопке вместе с русской «э», а также «`» на периферийной кнопке с буквой «ё».Ни один из этих символов не используется при нормальном, грамотном наборе текста. Однако, нельзя отрицать важность символов «'» и «"» при программировании и вёрстке HTML, чего мы делать и не будем.
| ' | U+0027 | апостро́ф | Этот знак действительно называется «APOSTROPHE» в Unicode, находится там, потому что так исторически сложилось в кодировке ASCII. Стандарт Unicode специально подчёркивает, что символ U+0027 имеет широкое использование, а собственно в роли апострофа должен выступать другой знак, о котором речь пойдёт ниже. |
| " | U+0022 | кавычка | Просто «кавычка», «QUOTATION MARK». Имеет широкое использование, но в качестве собственно текстовых кавычек рекомендованы другие символы, о которых речь также пойдёт ниже. |
| ` | U+0060 | гра́вис | Гравис используется для того, чтобы акцентировать гласные в некоторых европейских языках: французском (déjà vu), итальянском (virtù), португальском, валлийском (mẁg) и других. Таким образом, гравис совершенно не употребляется в современном русском языке, а также не имеет никакого отношения к апострофам или кавычкам. |
Я предлагаю называть по-русски «'» стандартным или машинописным апострофом, «"» — стандартной или машинописной кавычкой, а «`», как ему и положено, грависом.
О кавычках я писал в статье Оформление цитат на сайтах, но будет нелишним напомнить ещё раз, поразвёрнутее.| « | U+00AB | открывающая кавычка-ёлочка | Вот они, настоящие, правильные, традиционные кавычки-ёлочки. Именно так должны выглядеть основные кавычки в русскоязычном текстовом наборе. Они не должны отбиваться пробелами от текста, который они окружают. |
| » | U+00BB | закрывающая кавычка-ёлочка | |
| „ | U+201E | открывающая кавычка-лапка | А это — настоящие традиционные кавычки второго рисунка, „лапки“. Именно так должны выглядеть вложенные кавычки в русскоязычном текстовом наборе. Они также не отбиваются пробелами от окружённого ими текста. Так уж сложилось, что кавычки-лапки заимствованы из немецкой типографики, а Unicode базировался на типографике американской. Поэтому наша открывающая кавычка называется в Unicode просто «двойной нижней из девяток» (потому что запятые обращены вниз и похожи на две цифры 9), а наша закрывающая кавычка наоборот называется «двойной открывающей». |
| “ | U+201C | закрывающая кавычка-лапка | |
| ‘ | U+2018 | открывающая ма́рровская кавычка | «Марровская» — это, пожалуй, жаргонизм. Правильно эти кавычки называются английскими одинарными. Эти кавычки используются только в филологии, где их ввёл в первой половине XX века академик Н. Я. Марр. Они используются для того, чтобы обозначить некоторое слово, значение слова или его происхождение («от латинского appellatio ‘сообщение’», «со словом ‘посёлок’ не склоняется»). Найти марровские кавычки можно в любом содержательном словаре, но обычному человеку (не филологу) эти кавычки употреблять не нужно, потому что незачем. В некотором смысле, это узкоспециальные знаки. |
| ’ | U+2019 | закрывающая ма́рровская кавычка |
Стоит упомянуть, что в шрифте Verdana в MS Windows (в том числе и в версии 5.01) закрывающая кавычка-лапка (она же открывающая двойная английская кавычка) имеет неправильный рисунок (штрихи развёрнуты вниз, а не вверх), так что не пугайтесь.
| ’ | U+2019 | апостро́ф | Кажется, мы это только что видели? Бинго! Для апострофа Unicode рекомендует к использованию тот же самый символ, который является английской одинарной закрывающей кавычкой (он же — закрывающая марровская кавычка). |
Я предлагаю называть этот апостроф традиционным апострофом, в отличие от стандартного (машинописного) апострофа. Традиционный апостроф включён в ряд «типографских» раскладок клавиатуры и доступен для набора с клавишей AltGr.
Наверное, стоит упомянуть, что в Unicode есть ещё апостроф-буква (U+02BC), который имеет семантику именно буквы, а не орфографического знака. Апостроф используется в качестве буквы в некоторых языках, но к русскому это отношения не имеет.
| ´ | U+0301 | знак ударения, аку́т | Знак ударения используется, чтобы отличать слова «стои́т» и «сто́ит», «больша́я» и «бо́льшая», «уже́» и «у́же», и так далее. Разумеется, акут надо ставить только в том случае, когда возможны разночтения. Ина́че э́то бу́дет похо́же на де́тский буква́рь. Знак ударения, естественно, ставится над ударной буквой. Символ U+0301 при наборе ставится после гласной, на которую падает ударение, как и любой другой комбинирующийся символ Unicode. |
Вообще говоря, проблема решается обновлением шрифта до версии 5.01, Verdana этой версии правильно обрабатывает диакритики. Для обновления можно скачать European Union Expansion Font Update, который доводит Verdana до версии 5.01 и решает проблему в Windows XP и Vista. Также приведу ссылку на скачивание отдельно шрифта Verdana 5.01 в формате TTF.
| ′ | U+2032 | одинарный штрих | Одинарный штрих используется для обозначения угловых минут, а двойной штрих — секунд (например, 59° 57′ 00″). Напомню, что в такой записи знаки градуса, минуты и секунды не отбиваются пробелами от предшествующего числа, а от последующего отбиваются тонкой шпацией  . |
| ″ | U+2033 | двойной штрих |
Возможно, в связи с проникновением компьютерных технологий в современную жизнь и общей глобализацией, одинарный и двойной штрихи приживутся в качестве сокращений для фута и дюйма в тесном наборе, но в обычных текстах я рекомендую писать слова «фут» и «дюйм» полностью.
habrahabr.ru










