Класс пружин жесткости
Примеры решения задач по теме «Силы упругости. Закон Гука»
«Физика - 10 класс»
При решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается.
Задача 1.
При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м.
Р е ш е н и е.
Согласно закону Гука, выражающему связь между модулем внешней силы , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
Для нахождения силы воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m.
Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g).
Следовательно,
Задача 2.
Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте.
Р е ш е н и е.
На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m + + yпp = 0.
Запишем это условие в проекциях на оси ОХ и OY:
Из первого уравнения системы получим Fyпp = mg sinα.
При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 - sinα1) = 5 • 10 • (0,866 - 0,5) (Н) = 18,3 Н.
Задача 3.
К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость).
Р е ш е н и е.
Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука
Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины.
Условие равновесия груза запишем в виде mg = k2х2.
Из этого уравнения найдём удлинение
Подставив выражение для х2 в уравнение (1), получим для удлинения
Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:
Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим
Для эффективной жёсткости получим выражение
Задача 4.
Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.
Р е ш е н и е.
На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити.
На гирю действуют сила тяжести и сила натяжения пружины.
Согласно второму закону Ньютона для бруска и гири запишем:
m11 = m1 + + ; m22 = m + упр.
В проекциях на выбранные оси координат запишем: на ось ОХ: m1а1 = Т;
на ось OY:
Так как нить нерастяжима, то модули ускорений равны: а1 = а2 = а.
В силу условия малых масс пружины, нити и блока можно записать: T2 = Fупр и Т1 = Т2 = Т.
Учтя последние равенства, систему уравнений (1) запишем в виде
Выразив ускорение из первого уравнения системы и подставив его во второе, получим
Из этого уравнения найдём силу натяжения нити:
Так как согласно закону Гука Fупр = kx, то
Тогда удлинение пружины
Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика - Физика, учебник для 10 класса - Класс!ная физика
Основное утверждение механики --- Сила --- Инертность тела. Масса. Единица массы --- Первый закон Ньютона --- Второй закон Ньютона --- Принцип суперпозиции сил --- Примеры решения задач по теме «Второй закон Ньютона» --- Третий закон Ньютона --- Геоцентрическая система отсчёта --- Принцип относительности Галилея. Инвариантные и относительные величины --- Силы в природе --- Сила тяжести и сила всемирного тяготения --- Сила тяжести на других планетах --- Примеры решения задач по теме «Закон всемирного тяготения» --- Первая космическая скорость --- Примеры решения задач по теме «Первая космическая скорость» --- Вес. Невесомость --- Деформация и силы упругости. Закон Гука --- Примеры решения задач по теме «Силы упругости. Закон Гука» --- Силы трения --- Примеры решения задач по теме «Силы трения» --- Примеры решения задач по теме «Силы трения» (продолжение) ---
Устали? - Отдыхаем!
Вверх
class-fizika.ru
Лабораторная работа № 2 «Измерение жесткости пружины»
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости Fупр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины kср.
Результат измерения обычно записывается в виде выражения k = = kcp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (εk) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — εkk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
Поэтому
Средства измерения: 1) набор грузов, масса каждого равна m0 = 0,100 кг, а погрешность Δm0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
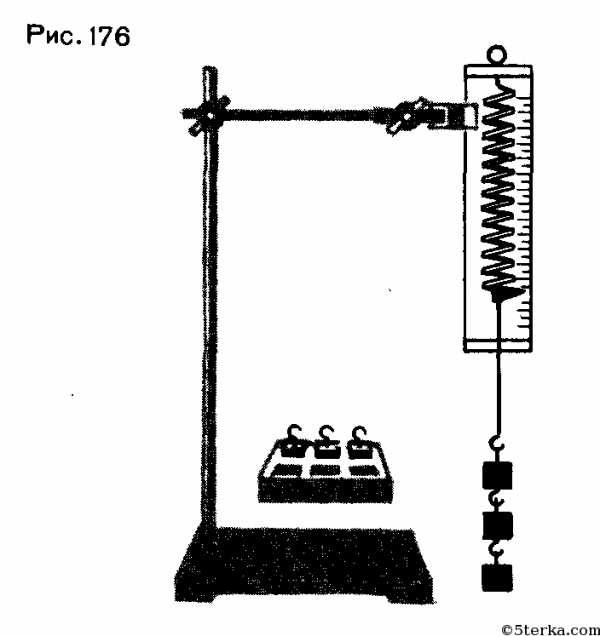
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
|
Номер опыта |
m, кг |
mg1, Н |
|х|, м |
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с2.
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F - приложенная к пружине сила, а х - изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
|
№ опыта |
масса, кг |
удлинение |х|, |
К, Н/м | |
|
м | ||||
|
1 |
0,1 |
1 |
0,036 |
27,78 |
|
2 |
0,2 |
2 |
0,074 |
27,03 |
|
3 |
0,3 |
3 |
0,112 |
26,79 |
|
4 |
0,4 |
4 |
0,155 |
25,81 |
* Ускорение свободного падения примем равным 10 м/с2.
Вычисления:

Вычисление погрешности измерения:
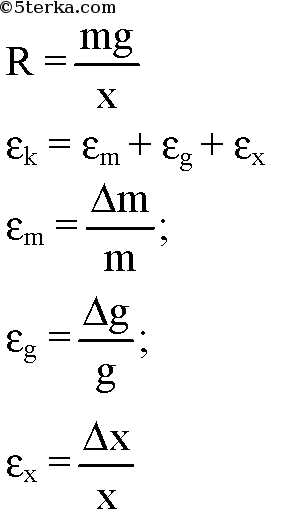
εх максимально когда х - наименьшее, т.е., в нашем случае, для опыта с одним грузом
Можно записать результат измерений как:
или округляя:
т.к. в нашем случае отклонения вычисленных R1; R2; R3; R4 от Rср велики из-за разности условий опытов принимаем
5terka.com
163 Классификация и характеристика пружин
Пружины и упругие элементы используют в конструкциях в качестве виброизолирующих, амортизирующих, аккумулирующих, натяжных, динамометрических и других устройств.
Классификация пружин: По виду воспринимаемой нагрузки различают:пружины растяжения, сжатия, кручения и изгиба.
По геометрической форме их называют: винтовыми, спиральными, прямыми и др.
В зависимости от назначения пружины бывают: силовыми (аккумуляторы энергии или движители), измерительными (упругие чувствительные элементы), амортизирующими и т. д.
В машиностроении наиболее распространены
винтовые цилиндрические пружины растяжения , сжатия и кручения.
Реже применяют специальные пружины:
тарельчатые и кольцевые – сжатия,
спиральные и стержневые- кручения; листовые (рессоры). пружины а - растяжения; б - сжатия; в - кручения; г - фасонные
а - тарельчатая; б- кольцевая; в - спиральная; г - стержневая; д - рессора
Общая характеристика пружин.
Пружины растяжения навивают без просветов между витками с начальным надавливанием витков, компенсирующим частично внешнюю нагрузку. Компенсирующее усилие составляет (0,25...0,3) Fnp,
где Fnp - предельное растягивающее усилие.
Для передачи внешней нагрузки пружины (диаметра до 3…4 мм) снабжают зацепами в форме отогнутых последних витков. Для ответственных пружин диаметром свыше 4 мм часто применяют закладные зацепы, но они менее технологичны.
Пружины сжатия навивают с просветом между витками, который должен на 10...20 % превышать осевые упругие перемещения каждого витка при наибольшей внешней нагрузке.
Пружины кручения навивают обычно с малым углом подъема и небольшими зазорами между витками (0,5 мм). Внешнюю нагрузку они воспринимают с помощью зацепов, образуемых отгибом концевых витков.
164 Основные параметры витых пружин. Материалы.
d - диаметр проволоки;
Do средний диаметр ;
Индекс c = Do/d;
n - число рабочих витков ;
Длина рабочей части -H0; шаг витков- t = Ho/h ;
Индекс пружины характеризует кривизну витка. Пружины с индексом С 3 применять не рекомендуется из-за высокой концентрации напряжений в витках. Его выбирают в зависимости от диаметра проволоки .
Основными материалами пружин являются высокопрочная специальная пружинная проволока, высокоуглеродистые стали, марганцовистая сталь, кремнистая сталь, хромованадиевая сталь и др.
Для работы в химически активной среде пружины изготовляют из цветных сплавов.
165 Расчет цилиндрических пружин
Напряжения в сечениях и деформации витков.
Под действием осевой растягивающей силы F в поперечном сечении пружины будет действовать поперечная сила F и момент Мz = FDo/2, плоскость которого совпадает с плоскостью пары сил F. Нормальное поперечное сечение витка наклонено к плоскости момента на угол а.
Проекции силы F на оси х, у и z и момент T равны:
Угол подъема витков мал поэтому можно считать, что сечение пружины работает лишь на кручение
Условие прочностной надежности пружины:
- максимальное касательное напряжение в сечении
где k — коэффициент, учитывающий кривизны витков; []— допускаемое касательное напряжение .
Wк— момент сопротивления сечения витка.
Для проволоки круглого поперечного сечения
Осевое перемещение пружины:
где - осевая податливость пружины.
Где — осевая податливость одного витка
Тогда Здесь G - модуль сдвига; Е — модуль упругости материала пружины
Диаметр проволоки, обеспечивающий необходимую прочность пружине
с заданным индексом с :
Если пружина сжатия установлена с предварительной затяжкой (нагрузкой) F1, то В зависимости от назначения пружины усилие F1 =(0,1 - 0,5) F2. Число витков округляют до полувитка при n 20; и до одного витка при n > 20.
Полное число витков n1 = n + (1,5...2). 1,5...2 витка идут на создание опорных поверхностей .
Полная длина ненагруженной пружины: При больших нагрузках и ограниченных габаритах используют составные пружины сжатия , навивку соседних пружин выполняют в противоположных направлениях (левом и правом).
Для предотвращения выпучивания пружины от потери устойчивости при больших значениях Ho/Do пружину следует ставить на оправках или монтировать в гильзах.
studfiles.net
Жесткость пружины | Блог Александра Воробьева
Опубликовано 14 Июн 2015Рубрика: Механика | 44 комментария
Максимальная сила сжатия или растяжения пружины не зависит от количества рабочих витков! Это означает, что если взять, например, цилиндрическую пружину сжатия, а затем разрезать её на две неравные по высоте части, то максимальное усилие при полном сжатии...
...обеих образовавшихся пружин будет одинаковым. Более того – максимальная сила останется такой же, как у исходной пружины!
В чем же тогда различие между тремя рассмотренными выше пружинами? Ответ на этот вопрос – в высотных размерах и жесткостях.
Меньшая пружина самая жесткая. У нее самый малый ход от свободного состояния до полного сжатия. Исходная пружина (до разделения) – самая мягкая. У нее самый большой ход.
Жесткость пружины (C) является ключевым параметром, определяющим силу сжатия или растяжения (Fi) при определенной величине деформации (L0— Li):
Fi=C*(L0— Li)
В свою очередь сама жесткость пружины (C) зависит только от жесткости одного витка (C1) и числа рабочих витков (N):
C=C1/N
Обратите внимание – жесткость одного витка всегда больше жесткости всей пружины! Причем, чем больше в пружине витков, тем она мягче.
Расчет в Excel жесткости витка пружины.
Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.
C1=G*X4/(Y*(D1— B)3)
В этой формуле:
G – модуль сдвига материала проволоки
Для пружинной стали:
G≈78500 МПа ±10%
Для пружинной бронзы:
G≈45000 МПа ±10%
X – минимальный размер сечения проволоки
Для круглой проволоки – это её диаметр:
X=D
Для прямоугольной проволоки:
X=H при H<B
X=B при B<H
H – высота сечения проволоки в направлении параллельном оси навивки пружины
B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины
Для круглой проволоки:
H=B=D
D1— наружный диаметр пружины
(D1— B) – средний диаметр пружины
Y – параметр жесткости сечения проволоки
Для круглой проволоки:
Y=8
Для прямоугольной проволоки:
Y=f(H/B)
Что это за функция — f (H/B)? В литературе она всегда задана в виде таблицы, что не всегда удобно, особенно для промежуточных значений H/B, которых попросту нет.
 Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
На графиках, представленных ниже, Excel нашел три уравнения для определения параметра Y при различных значениях аргумента — отношения высоты проволоки к ширине - H/B. Красные точки – это заданные значения из таблицы (столбец №2), черные линии – это графики найденных аппроксимирующих функций. Уравнения этих функций Excel вывел непосредственно на поля графиков.
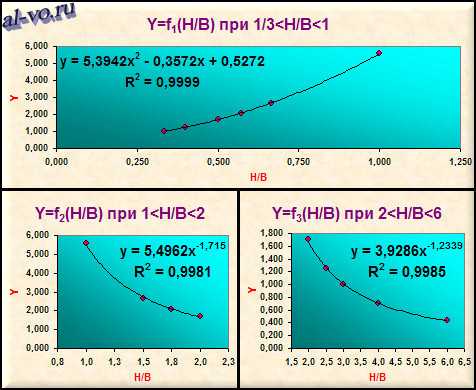
В таблице в столбце №3 размещены посчитанные по полученным формулам значения параметра жесткости сечения проволоки Y, а в столбцах №4 и №5 — абсолютные Δабс и относительные Δотн погрешности аппроксимации.
Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R2 очень близка к 1 и относительная погрешность не превышает 2,7%!
Применим на практике полученные результаты.
Расчет пружины сжатия из проволоки прямоугольного сечения.

Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.
Представленная ниже программа является переработанной версией программы расчета цилиндрических пружин из круглой проволоки, подробное описание которой вы найдете, перейдя по ссылке. Прочтите эту статью, и вам проще будет разобраться в алгоритме.
Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C1), задающей жесткость пружины (C) в целом.
Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.

4. I=(D1/B)-1
5. При 1/3<H/B<1: Y=5,3942*(H/B)2-0,3572*(H/B)+0,5272
При 1<H/B<2: Y=5,4962*(H/B)(-1.715)
При 2<H/B<6: Y=3,9286*(H/B)(-1.2339)
6. При H<B: C1=(78500*h5)/(Y*(D1— B)3)
При H>B: C1=(78500*B4)/(Y*(D1— B)3)
8. Tnom=1,25*(F2/C1)+H
9. Tmax=π*(D1— B)*tg (10°)
11. S3=T— H
12. F3=C1*S3
14. Nрасч=(L2— H)/(H+F3/C1— F2/C1)
16. C=C1/N
17. L0=N*T+H
18. L3=N*H+H
19. F2=C*L0— C*L2
21. F1=C*L0— C*L1
22. N1=N+1,5
23. A=arctg (T/(π*(D1— H)))
24. Lразв=π*N1*(D1— H)/cos (A)
25. Q=H*B*Lразв*7,85/106
Заключение.
Значение модуля сдвига (G) материала проволоки в существенной мере влияющее на жесткость пружины (C) в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.
Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…
Напишите пару строк в комментариях — мне всегда интересно ваше мнение.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так... — никаких паролей нет!
Ссылка на скачивание файла с программой: raschet-pruzhiny-szhatiya-iz-pryamougolnoy-provoloki (xls 94,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
Пружина
Вита цилиндрическая пружина растяжения
Пружина - упругий устройство используется главным образом для поглощения и накопления механической энергии.
1. Материалы для изготовления пружин
Обычно изготавливаются из закаленной стали. Стальные пружины общего потребления изготавливают из высокоуглеродистых сталей (У9А-У12А, 65, 70), легированных марганцем, кремнием, ванадием (65Г, 60С2А, 65С2ВА).
Для пружин, требующих большей коррозионной стойкости применяемых легированные стали и цветные металлы, такие как нержавеющая сталь (12Х18Н10Т), фосфористая бронза или титановые сплавы для пружин, которые должны быть токопроводящими - бериллиевая бронза (БРБ-2). В зависимости от конструкций и условий эксплуатации, можно использовать материал для создания пружины, имеющий необходимое сочетание механической жесткости и упругости: технически, деревянный лук является разновидностью пружины.
2. История
Витые конические пружины
Спиральная пружина в механизме часов
Пластинчатая пружина рессоры автомобиля
Тарельчатая пружина
Пружина Бурдона в конструкции манометра
Основные принципы пружины использовались еще несколько тысяч лет назад в механизмах, которые используют внезапную разрядку накопленной механической энергии, например лук или некоторые ловушки на животных (в форме сильно напряженных деревянных прутьев).
В римский период для метания снарядов использовалась упругость отогнутых досок (пример плоской пружины). Интересным был проект Леонардо да Винчи примерно 1485 по изготовлению гигантского арбалета для использования при осадах. Стоит упомянуть также и о миниатюрный арбалет из стали, изобретение испанских мавров XV вв. Его можно было легко спрятать даже в рукаве.
Около 1500 года пружина выступает в новой конструкции - спиральной пружины, которая начала играть роль источника энергии в часах. В 1616 году Веранцио Фаусто, автор книги о машинах, подал рисунок повозки на рессорах. После этого, как минимум через 50 лет стальные рессоры уже были в широком употреблении.
Винтовая пружина, вероятно, развилась со спиральной. Уже в конце XVIII века был построен станок для намотки таких пружин.
3. Классификация пружин
3.1. По виду нагрузки
1. Пружины сжатия, рассчитанные на уменьшение длины под нагрузкой. Витки таких пружин без нагрузки не касаются друг друга. Крайние витки поджимают к соседним и торцы пружины шлифуют до образования плоскости перпендикулярной к оси пружины. Длинные пружины сжатия, для предотвращения потери устойчивости, ставят на оправки или в стаканы.
2. Пружины растяжения, которые рассчитаны на увеличение длины под нагрузкой. В ненагруженном состоянии обычно сомкнуты витка. На концах для закрепления пружины изготовляют крючки или кольца.
3. Пружины кручения бывают двух видов:
- торсионные, которые выполняются в виде стержня, работающего на кручения (имеет большую длину, чем витая пружина)
- витые пружины, работающие на кручение (как в прищепка для белья или в мышеловках).
4. Пружины сгиба, которые изготавливают обычно в виде балки на двух опорах или консоли, работающей на изгиб.
5. Пружина Бурдона или трубчатая пружина в манометрах для измерения давления, выполняет роль чувствительного элемента.
3.2. По конструктивному исполнению
4. Свойства пружин
4.1. Закон Гука
Большинство пружин, не испытывают деформаций при пределом упругости) описываются законом Гука, согласно которому приложена сила, прямо пропорциональная линейном удлинение пружины относительно равновесного положения:
где
x - вектор смещения - расстояние и направление деформации пружины; F - результирующий вектор силы - величина и направление усилия, направленного на возвращение пружины к равновесному состоянию; k - коэффициент жесткости пружины (константа пружины).Цилиндрические пружины характеризуются устойчивым коэффициентом жесткости. Но есть конструкции пружин (например конические, тарельчатые, пластинчатые), коэффициент жесткости которых меняется по мере деформирования. В этом случае зависимость закону Гука усложняется и между усилием и деформацией проявляется нелинейная зависимость.
Энергия упругой деформации стержня или пружины выражается через коэффициент жесткости по формуле:
.4.2. Гармонические колебания
Деформация пружины, x, как функция времени. Время между двумя экстремумами называется - период колебанийПоскольку согласно вторым законом Ньютона усилия равен произведению массы тела на ускорение, то с учетом закона Гука можно записать:
Массой пружины является малой по сравнению с массой подвешенного тела пренебрегаем. Поскольку ускорение определяется как вторая производная перемещения по времени, можно записать:
Это линейное дифференциальное уравнение второго порядка для смещения х как функции времени. После перегруппировки можно записать
решением которого являются:
и константы, которые находятся с начальных условий (начальная деформация и начальная скорость массы). График этой функции при (Для нулевого положения груза) показано на рисунке.
4.3. Сочетание пружин
Зависимости для определения эквивалентных параметров при параллельном и последовательном соединении двух пружин сведены в таблицу
nado.znate.ru
Пружины - технические характеристики, напряжения, жесткость, расчет. - 6 Февраля 2014
Пружины
В трубопроводной арматуре используются пружины сжатия, кручения и растяжения. Наиболее частое применение находят цилиндрические винтовые пружины сжатия из проволоки круглого сечения. Эти пружины надежны в работе и технологичны в изготовлении. Пружины в конструкциях арматуры требуются для создания постоянных сил в целях обеспечения герметичности затвора (например, в предохранительных или перепускных клапанах) либо в целях создания требуемой зависимости ход — давление на пневмоприводе (в регулирующих клапанах). В остальных случаях пружины играют вспомогательную роль (защелки, фиксаторы и т.д.). В предохранительных муфтах или муфтах ограничения крутящего момента могут быть использованы пружины кручения. В некоторых случаях применяются и тарельчатые пружины, например в целях упругой компенсации тепловых деформаций удлинения шпинделей арматуры, работающей при повышенной температуре. Цилиндрические винтовые пружины. Пружины сжатия и растяжения регламентированы ГОСТ 13764—68—ГОСТ 13767—68. В трубопроводной арматуре наиболее часто используются пружины из проволоки диаметром 4—12 мм. В зависимости от выносливости — числа циклов N до разрушения — пружины подразделяются на три класса. В первый и второй класс входят пружины сжатия и растяжения, в третий—только пружины сжатия. Для первого класса выносливость пружины должна быть обеспечена в N ^ 5-10 циклов, для второго — в N ^ 10^ циклов и для третьего —в N ^ 2-10* циклов. Допускаемое напряжение в пружинах второго класса примерно в 1,5, а третьего класса примерно в 2,3 раза больше, чем в пружинах первого класса, что позволяет применять пружины меньших размеров, но при меньшей их выносливости. Применяемые в трубопроводной арматуре пружины для предохранительных, перепускных и редукционных клапанов, мембранных исполнительных механизмов и других ответственных конструкций можно отнести к пружинам второго класса.

Поскольку цикловая нагрузка пружин в арматуре обычно характеризуется незначительным изменением силы пружины, то, применяя соответствующие напряжения, можно обеспечить работу пружины в условиях неограниченной выносливости. По условиям ГОСТа, все статические пружины, длительно пребывающие в деформированном состоянии и периодически нагружаемые со скоростью Од менее tJ^pi относятся ко второму классу. Здесь Од — наибольшая скорость перемещения подвижного конца пружины при нагружений или разгрузке (м/с), о^р — критическая скорость пружин сжатия (м/с), соответствующая возникновению соударения витков пружины от сил инерции. Вводимые ГОСТ 13764—68 ограничения расчетных напряжений и свойств проволоки обеспечивают неограниченную стойкость статических пружин при остаточных деформациях не более 15 % от значения максимальной деформации Fg (рис. 5.16). Каждый класс пружин подразделяется на разряды. Во втором классе содержится четыре разряда, причем к четвертому разряду относятся только пружины сжатия, к остальным —пружины сжатия и растяжения. Основные технические характеристики пружин второго класса приведены в табл. 5.11. При расчете пружин для наглядности используются диаграммы зависимости силы пружины Рот деформации (рис. 5.16), которые применяются для последовательного определения параметров пружины. Действительная (уточненная) характеристика несколько отличается от линейной. При длинных пружинах жесткость пружины с увеличением деформации несколько снижается в связи с уменьшением наклона витков, при коротких пружинах, используемых, например, в регулирующих клапанах, наоборот, жесткость пружины с увеличением деформации увеличивается в связи с уменьшением числа рабочих витков. Допускаемые напряжения в пружинах обычно имеют большие значения и принимаются в пределах: для стали —от 400 до 1350 МПа, для бронзы —от 300 до 450 МПа. Допускаемое напряжение зависит от материала проволоки и ее диаметра, так как проволока малого диаметра благодаря процессу волочения приобретает повышенные механические свойства. Для катаного материала допускаемое напряжение не зависит от диаметра. Допускаемые значения напряжений, рекомендуемых для расчета пружин из различных материалов, приведены в табл. 5.12—5.14.
5.11. Технические характеристики пружин второго класса по Гост 13.764—68
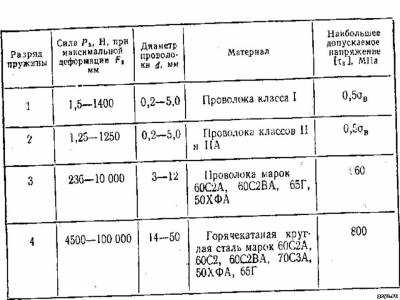
5.12. Допускаемые значения напряжений в пружинах для арматуры, изготовляемых из углеродистой пружинной стали (материал пружин: проволока диаметром d = 0,2-8,0 мм из углеродистой пружинной стали, холоднотянутая без термообработки. Допустимые условия эксплуатации пружин без покрытий: атмосфера с нормальной влажностью при температуре от —40 до +120 L)
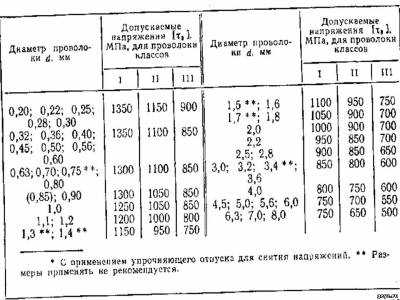
5.13. Допускаемые значения напряжений в пружинах для арматуры, изготовляемых из легированной стали
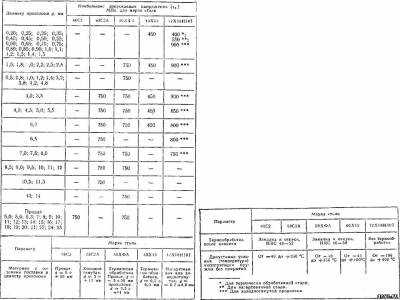
5.14. Допускаемые значения напряжений в пружинах для арматуры, изготовляемых из бронзы [материал пружин: проволока диаметром Дп = 0,2-12 мм бронзовая нагартованная (в состоянии поставки)]
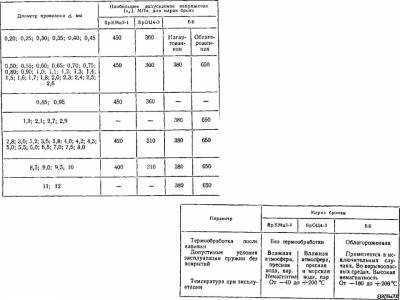
Пружины, изготовленные из углеродистой холоднотянутой стали, подвергаются упрочняющему отпуску для снятия напряжений при температуре 240—260 °С с выдержкой в 10—30 мин в зависимости от диаметра проволоки. Охлаждение производится на воздухе. Пружины из легированной стали подвергаются закалке с охлаждением в масле. Температура нагрева для стали марки 6GC2A равна 820 —840 °С, для стали марки 50ХФА —850—860 °С, для стали марки 40X13 — 1000—1100 °С. Выдержка при нагреве должна быть в пределах от 8 до 30 мин в зависимости от диаметра проволоки пружины. После закалки пружины из легированной стали подвергаются отпуску в соляной ванне с нагревом стали марки 6GC2A до 400—425 °С — для получения твердости HRC 48—52, стали марки 50ХФА до 400—420 °С — для получения твердости HRC 46 —50 и стали марки 40X13 до 480—495 °С — для получения твердости HRC 46—50. Пружины из стали марки 12Х18Н10Т подвергают упрочняющему отпуску для снятия внутренних напряжений при температуре 400—430 "С с выдержкой 20—30 мин и охлаждением на воздухе. Пружины из проволоки марки БрКМцЗ—I подвергают упрочняющему отпуску для снятия напряжений при температуре 120—150 °С с выдержкой в течение I—2 ч и последующим охлаждением на воздухе. Пружины из бериллиевой бронзы марки ББ подлежат закалке с охлаждением в воде комнатной температуры. Нагрев перед закалкой до 780 °С с выдержкой 1—2 ч. После закалки производится облагораживание при температуре 325 °С с выдержкой 2—5 ч в зависимости от диаметра проволоки пружины. Для стабилизации размеров пружин, изготовленных из закаливаемых сталей, предварительной проверки качества материала и результатов термической обработки пружины непосредственно после закалки и отпуска подвергаются «заневоливанию» в течение 6 ч путем сжатия пружины до соприкосновения витков. Пружины, изготовленные из углеродистой холоднотянутой стали без закалки после навивки, после упрочняющего отпуска для снятия напряжений подвергают заневоливанию в течение 6 ч либо взамен этого производят 3—5-кратное сжатие пружины до соприкосновения витков. Антикоррозионные и электролитические покрытия пружин и прогревы, выполняемые после покрытий в целях удаления водорода, могут быть источником возникновения хрупкости пружины, поэтому такие пружины после покрытий подвергаются заневоливанию в течение 24 ч до соприкосновения витков. В тех исключительных случаях, когда заневоливание путем сжатия пружины до соприкосновения витков недопустимо из-за чрезмерно больших напряжений, которые могут возникнуть, заневоливаиие производится на величину наибольших деформаций, создаваемых в пружине при ее работе в конструкциях арматуры. Пружина сжатия работает под действием осевой нагрузки, поэтому при проектировании следует предусмотреть ее продольную устойчивость против бокового выпучивания. Она зависит от отношения длины пружины Яо в свободном состоянии к среднему диаметру Do пружины (HQIDQ) и от способа закрепления конечных витков, определяющего возможность поворота крайних вит¬ков пружины. Различают два случая закрепления (рис, 5.17): случай, когда конечные витки имеют возможность поворота относительно вертикальной оси; допускается условие HJDo Сила, действующая на пружину сжатия, вызывает в каждом из поперечных сечений проволоки пружины суммарное напряжение от среза и кручения, определяемое формулой

Рис. 5 17, Схемы закрепления конечных витков пружины сжатия
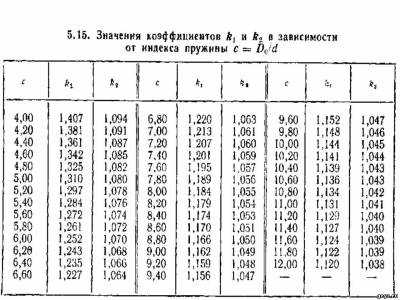
5.16. Сила пружины и жесткость одного витка (изменение силы при изменении деформации одного витка на 1 мм) для пружин сжатия или пружин растяжения (материал — сталь, С = 80000 МПа)

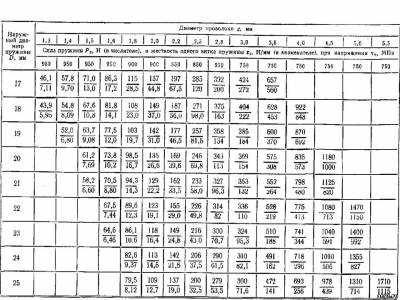
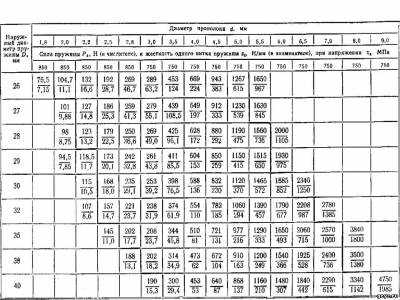
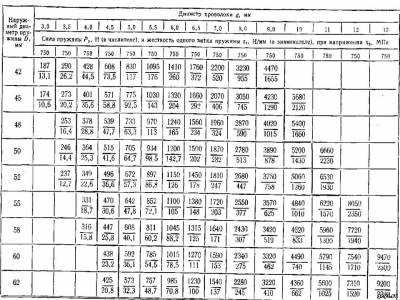
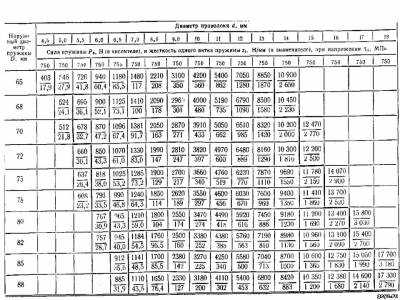


Шаг витков пружины i, мм, определяется в зависимости от максимальной деформации одного витка, мм. При рабочей деформации пружины под действием силы между витками должен быть сохранен зазор, значение которого обычно принимается 6 ^ 0,2d при d 5 мм. Обычно шаг пружины находится в пределах Do . D, Расчет пружин можно производить с использованием данных табл. 5.16 и номограмм, приведенных на рис. 5.18 и 5.19. Предварительными исходными данными, которыми задаются при выборе и расчете пружин, обычно являются следующие: наружный диаметр пружины D, мм; сила пружины Р^, И (при предварительной деформации F^) и сила Р2, Н (при рабочей деформации F2), а также рабочий ход пружины h = — Fi, мм. В зависимости от назначения и условий работы пружины могут быть заданы дополнительные ограничения в жесткости пружины или ее габаритных размерах. Ниже приведена методика расчета пружины для одного из часто встречающихся на практике случаев. Заданы: сила пружины Pi, Н, при предварительной деформации; сила пружины Pg, Н, при рабочей деформации; рабочий ход пружины h, мм; наружный диаметр пружины D, мм. Решение. 1. Выбирают материал для изготовления пружины исходя из условий ее эксплуатации, степени ответственности, температурного режима и т. п. 2. Задаются наибольшим допускаемым для данного материала напряжением Тд, МПа, и модулем сдвига металла G, МПа. 3. Определяют необходимое значение силы Pg при сжатии пружины до соприкосновения витков. Обычно принимают Pg = 1,25Р2, для ответственных пружин принимают Pg = bSPg. 4. Пользуясь табл. 5.16, предварительно выбирают диаметр проволоки d по величинам Pg и D с учетом соотношения между принятым допускаемым напряжением Тд и напряжением Тд ^абл (в табл. см, Тд). 5. Определяют действительное напряжение в проволоке пружины.
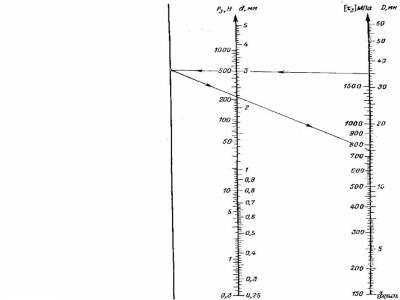
Рис. 5.18. Номограмма для определения силы Р в пружинах сжатия пример. Дано: диаметр проволоки d = 3 мм, наружный Диаметр пружины i3 = 35 мм, допускаемое напряжение iTjl = = 750 МПа. Решение: = 220 Н

Рис. 5.19. Номограмма для определения жесткости г пружины сжатия Пример Дано: диаметр проволоки Dп = 3 мм, наружный диаметр пружины D = 35 мм, число рабочих витков п = ~ 10. Решение: жесткость пружины г = 2,4 Н/мм

geyz.ru